Längeneinheiten
Die Basiseinheit für Längen ist das Meter. Für größere oder kleinere Längen verwendet man Einheiten, die durch Vervielfachen mit Zehnerpotenzen aus dem Meter abgeleitet sind, wie z. B. Kilometer (km), Dezimeter (dm), Zentimeter (cm), Millimeter (mm), Mikrometer (µm), Nanometer (nm).
Die Basiseinheit für Längen ist das Meter. Für größere oder kleinere Längen verwendet man Einheiten, die durch Vervielfachen mit Zehnerpotenzen aus dem Meter abgeleitet sind, wie z. B. Kilometer (km), Dezimeter (dm), Zentimeter (cm), Millimeter (mm), Mikrometer (µm), Nanometer (nm).
An nichtmetrischen Maßen sind heute noch gebräuchlich:
In der Seefahrt:
Seemeile (sm) 1 sm = 1,851,2 km
In Großbritannien und den USA:
| statute mile (st.mi.) | 1 st.mi. = 1609,3 km |
| yard (yd.) | 1 yd. = 0,9144 m |
| foot (ft.) | 1 ft. = 0,3048 m |
| inch (in.) | 1 in. = 2,54 cm |
Zwischen den Einheiten gelten folgende Beziehungen:
1 st.mi. = 5280 ft.
1 yd. = 3 ft.
1 ft. = 12 in.
Der Inch entspricht dem alten deutschen Maß Zoll (Zollstock).
-
Messgeräte für Längenmessung

B. Mahler, Fotograf, Berlin
-
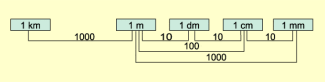
Übersicht über die Umrechnung von Längeneinheiten