Parallelogramm
Ein Viereck, dessen gegenüberliegende Seiten parallel sind, heißt Parallelogramm. Die gegenüberliegenden Seiten sind demzufolge gleich lang. Die Diagonalen in einem Parallelogramm halbieren einander. Die gegenüberliegenden Winkel sind gleich groß.
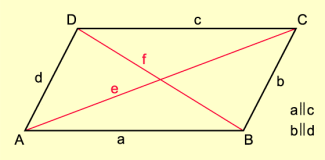
Ein Viereck, dessen gegenüberliegende Seiten parallel sind, heißt Parallelogramm (Bild 1).
Die gegenüberliegenden Seiten sind demzufolge gleich lang. Die Diagonalen in einem Parallelogramm halbieren einander.
Die gegenüberliegenden Innenwinkel sind gleich groß.
-
Parallelogramm
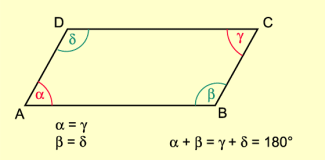
Im Parallelogramm ergänzen sich je zwei benachbarte Innenwinkel zu (Bild 2).
Ein Parallelogramm ist ein Rechteck, wenn benachbarte Seiten einen rechten Winkel bilden oder die Diagonalen gleich lang sind.
Ein Parallelogramm ist eine Raute (ein Rhombus), wenn die Seiten gleich lang oder die Diagonalen senkrecht zueinander sind.
-
Winkel im Parallelogramm
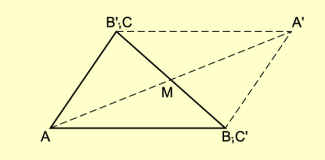
Ein Parallelogramm lässt sich durch Spiegelung eines beliebigen Dreiecks am Mittelpunkt einer Dreiecksseite konstruieren (Bild 3).
Ein Parallelogramm ist punktsymmetrisch bezüglich des Diagonalenschnittpunkts M.
-
Spiegelung eines Dreiecks
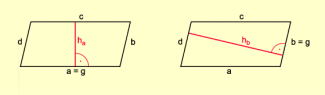
Der Abstand zweier paralleler Seiten heißt Höhe h des Parallelogramms. Jedes Parallelogramm besitzt zwei Höhen. Die Seite, zu der die Höhe senkrecht steht, heißt Grundseite g des Parallelogramms (Bild 4).
Jedes Parallelogramm kann durch Zerlegen in ein flächeninhaltsgleiches Rechteck umgewandelt werden.
Der Flächeninhalt des Rechtecks lässt sich mit der Gleichung berechnen. Da das Parallelogramm den gleichen Flächeninhalt besitzt, kann dieser aus der Grundseite a und der Höhe berechnet werden.
Es gilt also auch hier:
bzw.
Allgemein gilt dann:
Der Flächeninhalt eines Parallelogramms ist gleich dem Produkt aus einer Seitenlänge und der Länge der zugehörigen Höhe.
Da im Parallelogramm die gegenüberliegenden Seiten gleich lang sind, wird der Umfang des Parallelogramms wie beim Rechteck berechnet:
u = a + b + c + d
bzw. mit a = c und b = d
u = 2(a + b)
-
Höhen im Parallelogramm
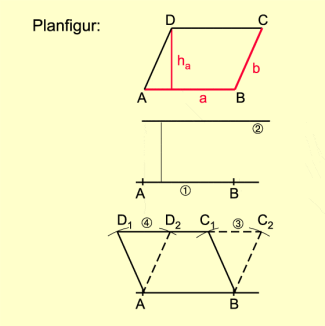
Für die Konstruktion eines Parallelogramm sind drei voneinander unabhängige Angaben notwendig (Bild 5).
Beispiel:
Gegeben sind die Längen der beiden Seiten a und b sowie der Höhe .
- Auf einer Geraden wird die Strecke AB mit abgetragen.
- Zur Geraden AB wird eine Parallele im Abstand gezeichnet.
- Um A und um B werden Kreisbogen mit dem Radius b gezeichnet. Es entstehen jeweils zwei Schnittpunkte der Kreisbogen mit der Parallelen.
- Verbindet man die entsprechenden Punkte, so entstehen zwei Parallelogramme .
Diese Konstruktion ist nicht eindeutig ausführbar.
-
Konstruktion eines Parallelogramms