Primzahlen, Historisches
Schon die Mathematiker der Antike suchten nach einem Verfahren zum Finden von Primzahlen. Bekannt ist ERATOSTHENES (um 230 v. Chr.) der mit dem nach ihm benannten Sieb eine Methode angab, die Primzahlen der Reihe nach zu ermitteln.
Auch PIERRE DE FERMAT, LEONHARD EULER und MARIN MERSENNE haben viel zur Erforschung der Primzahlen beigetragen.
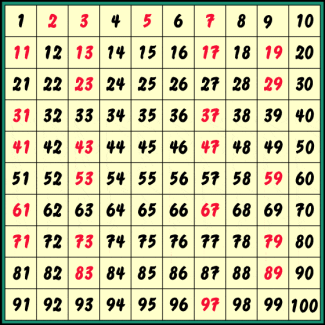
Schon die Mathematiker der Antike suchten nach einem Verfahren zum Finden von Primzahlen. Bekannt ist ERATOSTHENES (um 230 v. Chr.) der mit dem nach ihm benannten Sieb eine Methode angab, die Primzahlen der Reihe nach zu ermitteln. Dazu ordnet man die Zahlen etwa wie im Bild 1 an.
Man beginnt nun oben links: 1 ist zu streichen und 2 als erste Primzahl einzukreisen. Nun streicht man alle Vielfachen von 2, also jede 2. Zahl. Dann nimmt man die nächste nicht gestrichene Zahl, also die 3. Dies ist die zweite Primzahl. Man streicht nun jede 3. Zahl und sucht dann die kleinste nicht gestrichene Zahl. Dies ist die 5. Nun ist jede 5. Zahl zu streichen. Setzt man dieses Verfahren fort, sind gerade die Primzahlen nicht durchs Sieb gefallen.
Auch MERSENNE (MARIN MERSENNE, 1588 bis 1648, französischer Mathematiker, Physiker und Musikwissenschaftler) hat sich – im Zusammenhang mit seinen Untersuchungen – zu den vollkommenen Zahlen intensiv mit Primzahlen befasst. So behauptete er, dass für die Zahl (mersennsche Zahlen) nur dann eine Primzahl ist, wenn p eine der Zahlen 1, 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 ist. Obwohl diese Behauptung falsch ist (für p = 61 ergibt sich eine Primzahl und für p = 67 ist m keine Primzahl), hat sie viel zur mathematischen Theoriebildung beigetragen.
-
Sieb des Eratosthenes
FERMAT stellte die Behauptung auf, dass alle Zahlen der Form Primzahlen sind. Für die ersten fünf Zahlen trifft dies zu:
EULER zeigte im Jahre 1732, dass die Behauptung falsch ist. Er fand heraus, dass das Produkt der Primzahlen 641 und 6 700 417 ist.
Mithilfe moderner Rechentechnik hat man versucht, immer neue Primzahlen zu entdecken. 1987 war die Zahl die größte bekannte Primzahl. Zu ihrer Darstellung werden rund 65000 Ziffern benötigt. Wollte man diese Zahl mit herkömmlichen Rechenmethoden finden, müsste man mehrere hundert Jahre rechnen.
Ein viel diskutiertes Problem war auch, ob man alle natürlichen Zahlen als Summen von Primzahlen darstellen kann. Heute weiß man, dass jede natürliche Zahl als Summe von höchstens 27 Primzahlen geschrieben werden kann.

