Regelmäßige Vielecke

Alle regelmäßigen Vielecke (n-Ecke) besitzen gleich lange Seiten und gleich große Innenwinkel und sind damit konvex.
Die Winkelsumme im n-Eck beträgt (n – 2) · 180°.
Im regelmäßigen n-Eck ist diese Winkelsumme gleichmäßig auf alle n Innenwinkel des n-Ecks verteilt.
Für die Größe jedes Innenwinkels in einem regelmäßigen n-Eck gilt:
$\frac{\left(n-2\right)\cdot 180°}{n}=180°-\frac{360°}{n}$

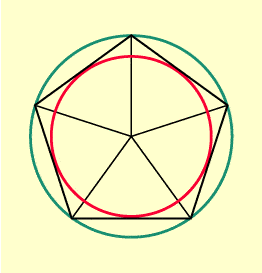
Jedem regelmäßigen n-Eck lassen sich ein Kreis einbeschreiben und ein Kreis umbeschreiben. Die Seiten des n-Ecks sind Sehnen des Inkreises und zugleich Tangenten des Umkreises (Bild 2).

Inkreis und Umkreis besitzen denselben Mittelpunkt. Dieser Mittelpunkt ist (als Umkreismittelpunkt) für ein gegebenes n-Eck konstruierbar:
Weil jede Seite des n-Ecks Sehne des Kreises ist, geht ihre Mittelsenkrechte durch den Mittelpunkt des Kreises.

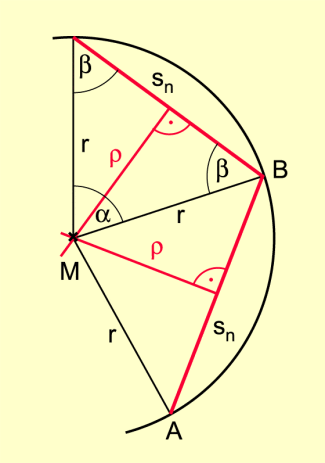
Verbindet man den Mittelpunkt des Umkreises mit jedem Eckpunkt, so wird das n-Eck in n gleichschenklige, zueinander kongruente Dreiecke zerlegt. Für die Winkel der Dreiecke gilt (Bild 3):
$\alpha =\frac{360°}{n}$(der n-te Teil des Vollwinkels) und

$\beta =\frac{180°-\alpha }{2}=90°-\frac{180°}{n}$

Damit ist der Innenwinkel des n-Ecks 2 · $\beta$.
Für den Radius r des Inkreises gilt $r\cdot \cos \frac{\alpha }{2}=r\cdot \cos \frac{180°}{n}$,
wobei r der Radius des Umkreises ist.

Übersicht über regelmäßige n-Ecke

Hierbei ist r der Radius des Umkreises.