Untersuchen quadratischer Funktionen

Tabellenkalkulationsprogramme können sehr hilfreich sein, wenn Wertetabellen von Funktionen zu ermitteln oder Funktionsgraphen zu zeichnen sind. Zur grafischen Darstellung einer Funktion muss zuerst eine Wertetabelle aufgestellt werden. Mit den Zahlenpaaren der Tabelle wird dann ein Diagramm erstellt.

Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
Viel günstiger als andere Nachhilfe und schützt deine Daten.

Jetzt 30 Tage risikofrei testen

Tabellenkopf vorgeben, z. B. Zelle A1: x, Zelle B1: y
Darstellungsintervall festlegen, z. B. –3 ≤ x ≤ 3 mit der Schrittweite 0,5 (Spalte A)
Funktionswerte ermitteln: In Zelle B2 (der Zelle für den ersten Funktionswert) wird der Funktionsterm durch Verknüpfung von Zellen definiert. Dabei ist immer mit einem Gleichheitszeichen zu beginnen. Der Funktionsterm ist nun auf die gesamte Tabelle zu übertragen. Dazu wird Zelle B2 bis zum Ende der Tabelle (B14) aufgezogen. Es entstehen die Funktionswerte für das vorgegebene Intervall.
Grafische Darstellung mit einem zum Programm gehörenden „Diagrammassistenten“

Beispiel:
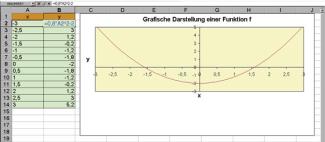
Erstellen einer Wertetabelle und grafische Darstellung der Funktion y = 0,8x² – 2 im Intervall –3 ≤ x ≤ 3 (Bild 1)

Ein einmal so angelegtes Rechenblatt kann später zur Darstellung einer anderen Funktion genutzt werden.
Wird in Zelle B2 der neue Funktionsterm definiert und auf die restlichen Felder der Wertetabelle übertragen, entsteht sofort die grafische Darstellung der neuen Funktion. So kann beispielsweise der Einfluss eines Parameters auf den Graphen einer Funktion experimentell untersucht werden. Anschaulicher wird die Untersuchung aber, wenn die grafische Darstellung der quadratischen Funktion für verschiedene Parameter in ein und demselben Koordinatensystem erfolgt. Dargestellt werden dann Kurvenscharen.

Beispiel:
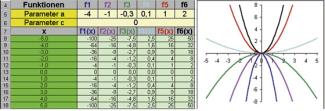
Es werden quadratische Funktionen der Form y = ax² + c untersucht. In einer ersten Versuchsreihe soll c = 0 gelten. Für den Parameter a werden die Werte –4; –1; –0,3; 0,1; 1; 2 verwendet. Die Funktionen f1 bis f6 werden durch Zellenverknüpfungen definiert, so entsteht z. B. in B8: B$5*A8^2+B$6 (Bild 2).

Werden Parameterwerte geändert, ändern sich unmittelbar die Funktionswerte in der Tabelle und auch die grafische Darstellung (Bild 3).

Lernhelfer (Duden Learnattack GmbH): "Untersuchen quadratischer Funktionen." In: Lernhelfer (Duden Learnattack GmbH). URL: http://www.lernhelfer.de/index.php/schuelerlexikon/mathematik/artikel/untersuchen-quadratischer-funktionen (Abgerufen: 21. May 2025, 06:21 UTC)

Suche nach passenden Schlagwörtern

Jetzt durchstarten

Entspannt durch die Schule mit KI-Tutor Kim und Duden Learnattack.

Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
Viel günstiger als andere Nachhilfe und schützt deine Daten.

Verwandte Artikel

Potenzfunktionen

Unter Potenzfunktionen werden Funktionen mit Gleichungen der folgenden Form verstanden:
$y = f (x) = x^{n} (x \in ℝ; n \in ℤ \ {0})$
Ihre Graphen nennt man Parabeln $(n > 0)$ bzw. Hyperbeln $(n < 0)$ n-ter Ordnung.

Streckung, Stauchung und Spiegelung von Graphen quadratischer Funktionen

Der Graph einer quadratischen Funktion mit der Gleichung $y = f (x) = a x^{2} + b x + c$ ist für a = 1 eine (ggf. verschobene) Normalparabel.
Für $a \neq 1$ erhalten wir als Graph im Vergleich zum Graphen von $y = f (x) = x^{2} + b x + c$ eine (in y-Richtung) gestreckte bzw. gestauchte und gegebenenfalls an der x-Achse gespiegelte Parabel.

Winkelfunktionen y = f(x) = a sin (bx + c)

Besonders bei der mathematischen Beschreibung von Schwingungsvorgängen wird häufig von Winkelfunktionen, speziell der Sinusfunktion mit Gleichungen der Form $y = f (x) = a \cdot \sin (b x + c)$ Gebrauch gemacht.
Bezogen auf den Graphen von f nennt man deshalb a auch die Amplitude der Sinuskurve, b deren Frequenz und c ihre Phasenverschiebung.

Funktionenscharen (Verschiebung, Streckung, Stauchung und Spiegelung von Funktionsgraphen)

In Funktionsgleichungen können Parameter in additiver und multiplikativer Verknüpfung mit Funktionstermen bzw. mit der Funktionsvariablen auftreten. Aus einer Funktionsgleichung $y = f (x)$ entstehen so z.B. die Gleichungen $y = f (x) + c$ , $y = f (x + d)$ , $y = a \cdot f (x)$ oder $y = f (b \cdot x)$ .
Diese Parameter haben Einfluss auf Eigenschaften und Verlauf der Graphen der Funktion.

Funktionsbegriff

Der Funktionsbegriff ist von zentraler Bedeutung für die gesamte Mathematik und spielt auch bei Anwendungen der Mathematik in Naturwissenschaft und Technik sowie in Wirtschaft und Gesellschaft eine wichtige Rolle. Seine Entwicklung zur heute gebräuchlichen Form hat Jahrhunderte gedauert. Die Namen bekannter Mathematiker sind mit diesem Prozess eng verbunden.
Unter einer Funktion f versteht man eine eindeutige Zuordnung (Abbildung), die jedem Element x aus einer Menge $D_{f}$ eindeutig ein Element y aus einer Menge $W_{f}$ zuordnet. $D_{f}$ heißt der Definitionsbereich, $W_{f}$ der Wertebereich der Funktion f. Man nennt $x \in D_{f}$ ein Argument, das zugeordnete Element $y \in W_{f}$ den Funktionswert von x bei der Funktion f. Als Kurzschreibweise gibt man die Funktionsgleichung u.a. in der Form $y = f (x)$ an.

Untersuchen quadratischer Funktionen

Schule wird easy mit KI-Tutor Kim und Duden Learnattack

Suche nach passenden Schlagwörtern