Winkel

Wie viele andere mathematische Begriffe bildete sich auch der Begriff „Winkel“ zur Beschreibung von Dingen oder Prozessen der Wirklichkeit heraus. Die Vielfalt der praktischen Anforderungen führte zur Entwicklung verschiedener Winkelbegriffe, welche jeweils unterschiedliche Seiten der Wirklichkeit betonen:

• Kommt es (etwa beim Neigungswinkel einer Böschung) auf die Beschreibung der Form oder der gegenseitigen Lage an, kann das durch zwei Strahlen mit gemeinsamen Anfangspunkt geschehen. Das führt zum Elementarwinkel, oft auch nur Winkel genannt.
• Wird eine Drehbewegung beschrieben, ist es sinnvoll, einen Strahl als den Anfangsstrahl und den anderen Strahl als den Endstrahl anzusehen und den Drehsinn der Bewegung zu beachten. Das führt zum Begriff des orientierten Winkels.
• Stehen dagegen vor allem die Aufteilung der Ebene in zwei Teilmengen oder die vom Strahl bei der Bewegung überstrichene Fläche im Mittelpunkt, führt das zum Begriff der Winkelfläche.

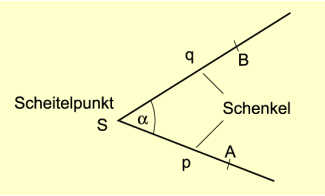
Zwei Strahlen mit gemeinsamem Anfangspunkt S bilden einen Winkel. Der gemeinsame Anfangspunkt ist der Scheitelpunkt des Winkels. Die zwei Strahlen sind die Schenkel des Winkels (Bild 1).
Bezeichnungsweisen (Bild 2):

• Griechischer Buchstabe: $\alpha$
• Angabe der Schenkel: $\sphericalangle$ (p, q) ist der durch die Strahlen p und q gebildete Winkel.
• Angabe dreier Punkte: $\sphericalangle$ ASB ist der Winkel mit dem Scheitelpunkt S und den Strahlen SA und SB als Schenkel.

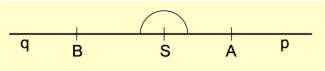
Gestreckter Winkel
Beide Strahlen liegen auf ein und derselben Geraden und haben nur den Punkt S gemeinsam (Bild 3).

Nullwinkel
Beide Strahlen p und q sind identisch (Bild 4).

Es ist ebenso möglich, die Flächen hervorzuheben:
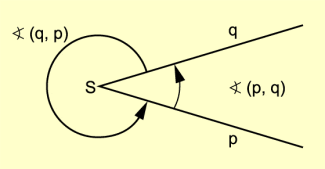
Die Strahlen p und q mit S als gemeinsamem Anfangspunkt teilen die Ebene in zwei Teilmengen.
Diese Teilmengen werden Winkelflächen (Winkelfelder) genannt und mit $\sphericalangle$ (p, q) und $\sphericalangle$ (q, p) bezeichnet.
Zur eindeutigen Bezeichnung ist vereinbart, dass die mit $\sphericalangle$ ( p, q) bezeichnete Winkelfläche immer entsprechend des positiven Drehsinns, d. h. entgegen des Uhrzeigersinns, beginnend beim Strahl p auszuwählen ist (vgl. Pfeilrichtung). Zu beachten ist, dass $\sphericalangle$ (p, q) $\ne$ $\sphericalangle$(q, p) ist.

Die Schenkel eines Winkels können auch als Original und Bild eines Strahls bei einer Drehung des Strahls um seinen Anfangspunkt angesehen werden:
Wird ein Strahl um seinen Anfangspunkt S gedreht, so entsteht ein orientierter Winkel. Der Drehpunkt S heißt Scheitelpunkt des Winkels Erfolgt die Drehung entgegen dem Uhrzeigersinn, so ist der Winkel positiv orientiert.
Der orientierte Winkel kann deshalb als geordnetes Paar zweier Strahlen mit gemeinsamen Anfangspunkt angesehen werden. Dabei ist, im Gegensatz zum (Elementar-) Winkel, einer der Strahlen als Anfangsstrahl hervorgehoben. Der Anfangsstrahl ist das Original bei der Drehung um S, der andere Strahl ist sein Bild.
Es ist folglich im Allgemeinen:
$\sphericalangle$ (p, q) $\ne$ $\sphericalangle$ (q, p)

Winkelgröße und Winkelarten
Winkel können hinsichtlich ihrer Größe miteinander verglichen werden.
Die Größe eines (Elementar-) Winkels ist die Klasse aller zueinander deckungsgleichen (kongruenten) Winkel. Zwei Winkel haben die gleiche Größe, wenn sie durch eine Kongruenzabbildung aufeinander abgebildet werden können.
Ob zwei Winkel gleich groß sind, kann man z. B. prüfen, indem man einen der Winkel auf Transparentpapier paust und das Bild auf den anderen Winkel legt. Man legt die Scheitelpunkte und einen der Schenkel aufeinander und versucht, nun auch das andere Paar Schenkel zur Deckung zu bringen. Gelingt das, sind beide Winkel gleich groß.
In der Praxis werden Winkel gemessen (Winkelmesser, Geodreieck) und ihre Größen verglichen. Alle Winkelmaße beruhen auf Teilungen des Kreises in 360 deckungsgleiche Teile (Kreisausschnitte).

Winkelarten
Winkel werden nach ihrer Größe unterschieden: