Wurzeln, Rechnen

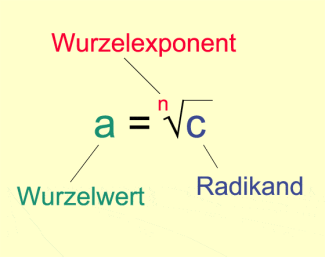
$a=\sqrt[n]{c}$ (gesprochen: a ist gleich n-te Wurzel aus c)
Dabei heißen n der Wurzelexponent, c der Radikand und a der Wurzelwert (Bild 1).
Im Bereich der reellen Zahlen existiert die n-te Wurzel aus c stets, wenn c eine nichtnegative reelle Zahl und n eine natürliche Zahl $\left(n>1\right)$ ist.

Wurzeln mit dem Wurzelexponenten 2 nennt man Quadratwurzeln und vereinbart, dass der Wurzelexponent nicht geschrieben werden muss:
$\sqrt[2]{a=}\sqrt{a}$

Wurzeln aus negativen Zahlen existieren im Bereich der reellen Zahlen nicht.

Die folgende Definition erlaubt es, Wurzeln als Potenzen zu schreiben:

$\sqrt[n]{a^m=}{a}^{\frac{m}{n}}\left(a>0;m,n\in \mathbb{N};m\ge 1;n\ge 2\right)$

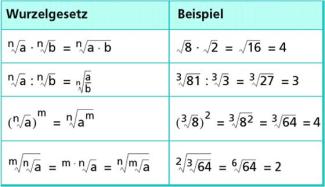
Beim Rechnen mit Wurzeln werden die in der Tabelle des Bildes 2 dargestellten Wurzelgesetze angewandt.
Zusätzlich zu diesen Wurzelngesetzen gilt:
$\sqrt[n]{1}=1\sqrt[n]{0}=0\sqrt[n]{a^n}=a\left(a>0\right)$