Exponentialfunktionen
Funktionen mit Gleichungen der Form
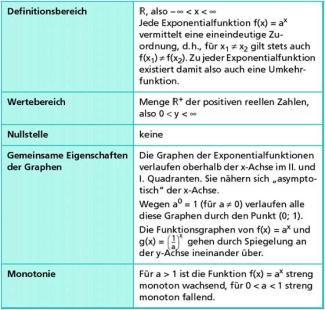
heißen Exponentialfunktionen. Ihr Definitionsbereich ist die Menge der reellen Zahlen.
Zur Förderung von Gärungsprozessen (etwa bei der Weinherstellung) werden Hefen eingesetzt. Die Hefezellen entwickeln sich in Nährlösungen. In einen Behälter wird beispielsweise 1 g Hefe gegeben. Aus Versuchen weiß man, dass sich die Anzahl bestimmter Hefezellen stündlich verdreifacht. Die folgende Tabelle gibt dann die Hefemasse an, die jeweils am Ende der genannten Zeiten vorhanden ist:
| Zeit t (in Stunden) | 0 | 1 | 2 | 3 | 4 | 5 |
| Hefemasse m (in Gramm) | 1 | 3 | 9 | 27 | 81 | 243 |
Da sich die Masse stündlich verdreifacht, gilt:
;
;
usw.
Also ist
Der dazugehörige Prozess wird wegen also durch die Gleichung beschrieben.
Definition: Funktionen mit Gleichungen der Form
heißen Exponentialfunktionen. Ihr Definitonsbereich ist die Menge der reellen Zahlen.
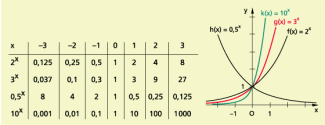
Um einen Überblick über einige elementare Eigenschaften dieser Funktionen zu erhalten, zeichnen wir unter Verwendung von Wertetabellen (Werte z. T. gerundet) die Graphen der in Bild 2 dargestellten Exponentialfunktionen
.
-
Beispiele für Exponentialfunktionen
Generell gelten für Exponentialfunktionen
die Eigenschaften nach Bild 3.
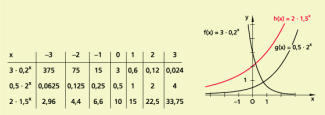
Die Exponentialfunktionen besitzen dieselben Eigenschaften wie die Funktionen mit Ausnahme des Schnittpunktes ihrer Graphen mit der y-Achse, der für der Punkt (0; c) ist. Der Graph der Funktion ergibt sich aus dem Graphen der Funktion f(x) = 2x durch Stauchung in Richtung der y-Achse auf das „0,5-Fache“ und der Graph von aus dem Graphen von entsprechend durch Streckung oder Stauchung in Richtung der y-Achse mit dem Faktor c.
-
Eigenschaften der Exponentialfunktion
Beispiele:
Insbesondere Wachstums- oder Abnahmeprozesse lassen sich mithilfe von Exponentialfunktionen beschreiben, z. B. der Bevölkerungszuwachs in einer Region, das Wachstum von Bakterienkulturen, der Kapitalzuwachs bei langjähriger Verzinsung, radioaktiver Zerfall bestimmter Elemente u. Ä.
Von besonderer Bedeutung ist die Exponentialfunktion in der die eulersche Zahl
e = 2,718 281 828 459 045 235 360 287 471 352 662 …
als Basis auftritt.
-
Beispiele für gestauchte und gestreckte Exponentialfunktionen
Der Schweizer Mathematiker LEONHARD EULER (1707 bis 1783) fand diese Zahl – einen unendlichen, nichtperiodischen Dezimalbruch – im Jahr 1727.

