Bilder an Sammellinsen
Sammellinsen sind durchsichtige Körper aus Glas oder Kunststoff, die sehr unterschiedliche Form haben können. Wenn Licht auf sie trifft, wird es nach dem Brechungsgesetz gebrochen. Dabei wird bei Sammellinsen auf sie fallendes achsenparalleles Licht hinter der Linse zunächst in einem Punkt, dem Brennpunkt, konzentriert. Für die Bildentstehung ist wesentlich, dass durch eine Linse jedem Gegenstandspunkt eindeutig ein Bildpunkt zugeordnet wird und somit ein scharfes Bild eines Gegenstandes entsteht. Je nach der Lage von Gegenstand und Linse kann dieses Bild unterschiedliche Lage und Größe haben. Es kann reell oder virtuell sein.
Grundsätzliches zur Bildentstehung
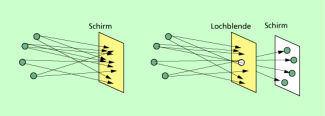
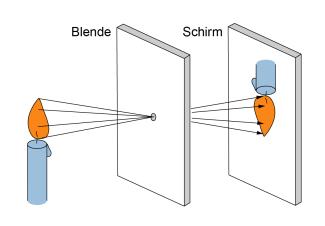
Bringt man einen Schirm in die Nähe eines beleuchteten Gegenstandes, dann kann man auf dem Schirm bestenfalls eine allgemeine Aufhellung, aber kein Bild des Gegenstandes beobachten (Bild 1 links). Das von jedem Gegenstandspunkt eines beleuchteten Körpers ausgehende Licht fällt auf die unterschiedlichsten Punkte des Schirms. Erst wenn der Strahlengang eingeschränkt wird, beispielsweise durch eine Blende (Bild 1 rechts) oder durch eine Linse, erhält man eine eindeutige Zuordnung zwischen Gegenstandspunkt und Bildpunkt und damit ein Bild. Damit kann man formulieren:
Das scharfe Bild eines Gegenstandes entsteht, wenn jedem Gegenstandspunkt eindeutig ein Bildpunkt zugeordnet werden kann.
Die einfachste Anordnung zur Erzeugung eines Bildes besteht darin, eine Blende in zweckmäßiger Entfernung vor einen Schirm zu setzen (Bild 2). Versieht man Blende und Schirm noch mit einem lichtundurchlässigen Gehäuse, dann hat man eine Lochkamera vor sich. Sie wird in größerer Form auch als Camera obscura (dunkle Kammer) bezeichnet.
Eine zweite Möglichkeit, eine solche eindeutige Zuordnung zwischen Gegenstandspunkt und Bildpunkt vorzunehmen, besteht in der Verwendung von Sammellinsen.
-
© Duden Learnattack GmbH
Sammellinsen und ihre Bauformen
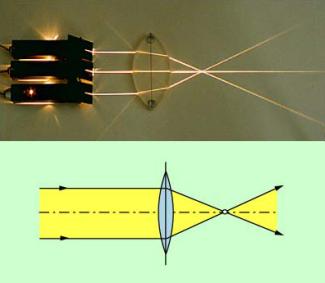
Sammellinsen sind durchsichtige Körper aus Glas oder Kunststoff, die sehr unterschiedliche Form haben können. Wenn Licht auf sie trifft, wird es nach dem Brechungsgesetz gebrochen. Sie sind dadurch charakterisiert, dass auf sie fallendes achsenparalleles Licht hinter der Linse zunächst in einem Punkt, dem Brennpunkt, konzentriert wird (Bild 3). Die Bezeichnung „Sammellinse“ kennzeichnet somit die optische Wirkung einer Linse.
-
L. Meyer, Potsdam
Sammellinsen aus Glas oder Kunststoff sind in der Mitte dicker als am Rand (Bild 2). Nach dieser äußerlich wahrnehmbaren Form bezeichnet man solche Sammellinsen auch als Konvexlinsen.
Beachte: Man kann nicht bei jeder Linse aus der äußeren Form erkennen, ob sie wie eine Sammellinse oder wie eine Zerstreuungslinse wirkt. Das gilt insbesondere für Linsen, die mit einer Flüssigkeit gefüllt sind oder die aus verschiedenen Stoffen bestehen.
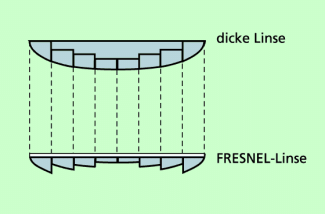
Eine besondere Form von Sammellinsen sind FRESNEL-Linsen , die nach dem französischen Physiker AUGUSTIN JEAN FRESNEL (1788-1827) benannt sind, der diese Art von Linsen entwickelt hat. FRESNEL-Linsen sind meist großflächige Linsen aus Kunststoff (Bild 5), die aufgrund ihres Aufbaus die gleiche brechende Wirkung wie dicke Glaslinsen haben. Es gibt sie als Sammellinsen oder als Zerstreuungslinsen. FRESNEL stellte fest, dass für die Stärke der Brechung des Lichtes durch eine Linse nicht die Dicke der Glasschicht entscheidend ist, sondern die Krümmung ihrer Oberfläche. Um eine genauso starke Krümmung und damit die gleiche Brechkraft wie bei einer dicken Linse zu erreichen, ging FRESNEL folgendermaßen vor:
| Die Linse wird, ausgehend von ihrer Mitte, in sehr kleine kreisförmige Bereiche (Kreisringe) unterteilt. Diese Bereiche sind sehr schmal und mit bloßem Auge kaum sichtbar. | |
| Die einzelnen Kreisringe erhalten an der Oberfläche genau die Krümmung, die eine dicke Linse an dieser Stelle hätte. |
Damit wird die gleiche Brechung des Lichtes erreicht wie mit einer entsprechenden dicken Linse. Mit modernen Kunststoffen kann man solche Linsen sehr dünn und großflächig herstellen. FRESNEL-Linsen werden vor allem dort genutzt, wo man preiswerte, dünne und großflächige Linsen benötigt, z.B. als Kondensorlinsen bei Tageslichtprojektoren oder als Lesehilfen.
Bildentstehung an Sammellinsen
Von jedem Punkt eines Gegenstandes geht Licht in die unterschiedlichsten Richtungen aus. Das Licht, das von einem Punkt P ausgeht und auf die Sammellinse fällt, trifft hinter der Linse wieder in einem Punkt P' zusammen (Bild 1). P' ist der Bildpunkt des Gegenstandspunktes P.
Um nun von einem Gegenstand das Bild zu erhalten, könnte man für alle möglichen Gegenstandspunkte die Bildpunkte konstruieren. Die Summe der Bildpunkte ergibt das Bild des Gegenstandes.
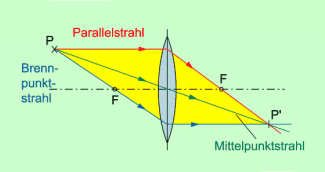
Zur zeichnerischen Konstruktion von Bildern reicht es aus, den Verlauf einiger charakteristischer Strahlen durch Sammellinsen zu kennen. Genutzt werden zur Bildkonstruktion Parallelstrahlen , Brennpunktstrahlen und Mittelpunktstrahlen (Bild 2).
Wenn diese Strahlen an einer dünnen Sammellinse gebrochen werden, so gilt unter der Bedingung achsennaher Strahlen:
| Ein Parallelstrahl wird so gebrochen, dass er dann durch den Brennpunkt verläuft. | |
| Ein Brennpunktstrahl wird so gebrochen, dass er dann parallel zur optischen Achse verläuft. | |
| Ein Mittelpunktstrahl geht ungebrochen durch eine Sammellinse. |
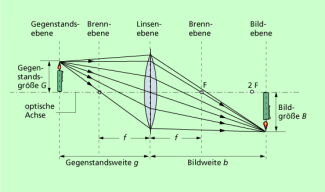
Diese drei charakteristischen Strahlen kann man zur Bildkonstruktion nutzen (Bild 7). Um einen Bildpunkt zu erhalten, reicht es aus, jeweils zwei Strahlen zu zeichnen. Fertigt man eine maßstäbliche Skizze an, so kann man aus der Zeichnung die Bildweite und die Bildgröße ermitteln.
Bringt man einen Schirm an die Stelle, an der sich die Strahlen schneiden, so erhält man auf dem Schirm ein scharfes Bild des Gegenstandes. Der Schirm befindet sich dann genau in der Bildweite. Verschiebt man den Schirm, so erhält man ebenfalls ein Bild. Es ist aber unscharf.
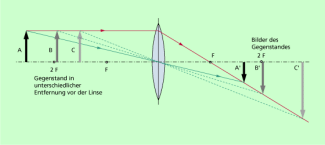
Was für ein Bild eines Gegenstandes durch eine Sammellinse entsteht, ist von der Gegenstandsweite (Entfernung Gegenstand-Linse) und von der Brennweite der Linse abhängig. Bild 8 zeigt einige Bilder eines Gegenstandes bestimmter Gegenstandsgröße bei unterschiedlicher Gegenstandweite. Ist die Gegenstandsweite größer als die Brennweite, entstehen reelle und umgekehrte Bilder unterschiedlicher Größe. Befindet sich der Gegenstand innerhalb der einfachen Brennweite, so entstehen virtuelle und aufrechte Bilder. Die Sammellinse wirkt als Lupe.
Die mathematischen Zusammenhänge zwischen Gegenstandsgröße, Bildgröße, Gegenstandsweite, Bildweite und Brennweite der Linse werden durch den Abbildungsmaßstab und durch die Abbildungsgleichung erfasst.
Für den Abbildungsmaßstab A gilt:
Die Abbildungsgleichung für dünne Linsen lautet:
Dabei ist zu beachten, dass die Brennweite von Sammellinsen im Unterschied zu der von Sammellinsen als positiver Wert angegeben wird. Eine Brennweite von f = +100 mm bedeutet: Es liegt eine Sammellinse mit einer Brennweite von 100 mm vor.
Der in Metern gemessene Kehrwert der Brennweite einer Linse wird als deren Brechkraft oder als Brechwert D bezeichnet. Es gilt somit:
Bei Brillen ist es üblich, die Brechkraft in Dioptrien (dpt) anzugeben. Eine Brechkraft von +2,5 dpt bedeutet dann: Es liegt eine Sammellinse mit einer Brennweite von vor.
Das fermatsche Prinzip bei Sammellinsen
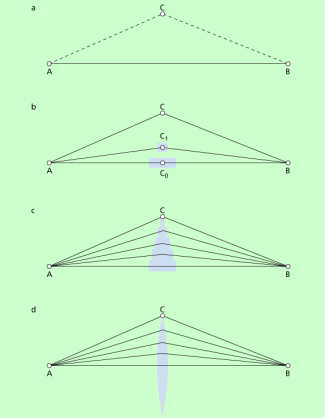
Nach dem fermatschen Prinzip legt das Licht den zeitlich kürzesten Weg zurück. Wenn Licht also von A nach B gesendet wird, so wird es den geraden Weg und niemals den Umweg über C wählen (Bild 9a).
Bringt man jedoch in die geradlinige Verbindung zwischen A und B bei ein Medium, in dem Licht sich langsamer ausbreitet, so kann durchaus der Weg über C der zeitlich kürzeste sein (Bild 9b).
Im Punkt muss dieses Medium nicht mehr ganz so breit sein, um dieselbe Verzögerung zu erreichen, weil nun der Weg ein wenig kürzer ist als der über (Bild 9c).
So kann man eine Figur aus diesem Medium konstruieren, damit alle Wege von A nach B gleich lang dauern, d.h. alle von A ausgehenden Lichtstrahlen durch dieses Medium in einem Punkt gesammelt werden. Dies ist die Sammellinse (Bild 9d).
Suche nach passenden Schlagwörtern
- Berechnung
- Lochkamera
- Bildgröße
- fermatsches Prinzip
- Brennpunktstrahlen
- Brennebene
- Gegenstandsweite
- Abbildungsmaßstab
- Bildweite
- Dioptrien
- Camera obscura
- Brennpunkt
- Sammellinsen
- Fresnellinsen
- Brechungsgesetz
- Linsenebene
- Brechkraft
- Parallelstrahlen
- Brechwert
- Abbildungsgleichung
- Gegenstandspunkt
- Bildpunkt
- Lupe
- Gegenstandsgröße
- Brennweite
- Rechenbeispiel
- Konvexlinsen
- Mittelpunktstrahlen
- Animation
- Fresnel-Linsen