Senkrechter Wurf

Für die Überlagerung von Bewegungen gilt das Unabhängigkeitsprinzip, das auch als Superpositionsprinzip bezeichnet wird. Es lautet:

Führt ein Körper gleichzeitig mehrere Teilbewegungen aus, so überlagern sich diese Teilbewegungen unabhängig voneinander zu einer resultierenden Gesamtbewegung.

Je nach der Richtung der Teilbewegungen unterscheidet man zwischen dem senkrechten Wurf nach oben und dem senkrechten Wurf nach unten.

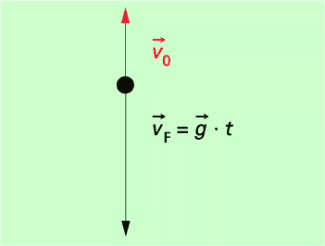
Senkrechter Wurf nach oben

Beim senkrechten Wurf nach oben überlagern sich eine gleichförmige Bewegung nach oben und der freie Fall in entgegengesetzter Richtung. Die Zeit bis zum Erreichen der maximalen Höhe, die Steigzeit, ergibt sich aus der Gleichung für die Geschwindigkeit, wenn man davon ausgeht, dass die Geschwindigkeit im obersten Punkt der Bahn null ist:
$\begin{array}{l}\text{Aus}v=v_0-g\cdot t\text{folgt mit}v=0:\\ v_0-g\cdot t=0\text{oder}\\ t=\frac{v_0}{g}\\ \text{Mit}t=t_h\text{erhält man:}\\ t_h=\frac{v_0}{g}\end{array}$

Die Steigzeit ist genauso groß wie die Fallzeit. Der gesamte Wurf ist damit doppelt so lang wie die Steigzeit.
Setzt man diese Steigzeit in die Gleichung für den Weg ein, so erhält man die maximale Höhe, die erreicht wird und die man als Wurfhöhe oder als Steighöhe bezeichnet:

$\begin{array}{l}\text{Aus}s=v_0\cdot t-\frac{g}{2}{t}^2\text{folgt mit}t=\frac{v_0}{g}:\\ s=v_0\cdot \frac{v_0}{g}-\frac{g}{2}\cdot {\left(\frac{v_0}{g}\right)}^2\\ s=\frac{v_0^2}{g}-\frac{v_0^2}{2g}=\frac{v_0^2}{2g}\\ \text{Mit}s=s_h\text{erhält man:}\\ s_h=\frac{v_0^2}{2g}\end{array}$

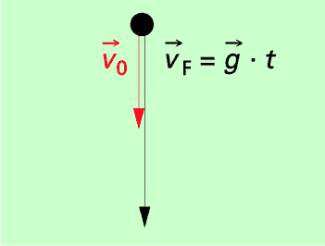
Senkrechter Wurf nach unten

Beim senkrechten Wurf nach unten überlagern sich eine gleichförmige Bewegung und der freie Fall. Beide Teilbewegungen haben die gleiche Richtung. Ein Beispiel dafür ist das senkrechte Hinunterwerfen eines Balles. Beim senkrechten Wurf nach unten addieren sich die Geschwindigkeiten beider Teilbewegungen (Bild 3) und in gleicher Weise die Wege.
Es gelten folgende Gesetze:

$\begin{array}{l}v=v_0+g\cdot t\\ s=v_0\cdot t+\frac{g}{2}\cdot t^2\end{array}$

Beachte: Alle genannten Gesetze gelten nur, wenn die Teilbewegungen senkrecht zueinander erfolgen und wenn bei der Fallbewegung der Luftwiderstand vernachlässigt werden kann.

Die Vorzeichen ergeben sich in Abhängigkeit vom gewählten Bezugssystem. Wählt man für den senkrechten Wurf nach unten das gleiche Bezugssystem wie für den Wurf nach oben (positive s-Richtung bzw. y-Richtung nach oben), so würden die Gleichungen für den Weg s und die Geschwindigkeit v lauten:

$s=-v_0\cdot t-\frac{g}{2}{t}^2\text{und}v=-v_0-g\cdot t$

Stimmt dagegen die positive s-Richtung bzw. y-Richtung mit der Bewegungsrichtung überein, so ergeben sich die weiter oben genannten Gleichungen mit positivem Vorzeichen. Da die Wahl des Bezugssystems willkürlich ist und verabredet werden muss, sind alle genannten Gleichungen richtig. Sie beziehen sich lediglich auf unterschiedliche Bezugssysteme.

Statt des Weges s setzt man wie bei anderen Würfen, die grafisch in einem x-y-Diagramm dargestellt werden, mitunter auch das Kurzzeichen y für den Weg in senkrechter Richtung ein.