Kinetische Energie
Kinetische Energie (Energie der Bewegung) ist die Fähigkeit eines Körpers, aufgrund seiner Bewegung mechanische Arbeit zu verrichten, Wärme abzugeben oder Licht auszusenden:
Formelzeichen: | ein Joule (1 J) ein Newtonmeter (1 Nm) |
Kinetische Energie ist eine spezielle Form mechanischer Energie.
Sich bewegende Körper, z. B. Radfahrer, ein fahrendes Auto, ein fallender Stein oder ein rotierendes Schwungrad besitzen kinetische Energie. Statt von kinetischer Energie spricht man auch von Energie der Bewegung oder Bewegungsenergie. Bei rotierenden Körpern nennt man die kinetische Energie auch Rotationsenergie. Allgemein gilt:
Kinetische Energie ist die Fähigkeit eines Körpers, aufgrund seiner Bewegung mechanische Arbeit zu verrichten, Wärme abzugeben oder Licht auszusenden:
| Formelzeichen: Einheiten: | ein Joule (1 J) ein Newtonmeter (1 Nm) |
Kinetische Energie ist eine spezielle Form mechanischer Energie. Die andere Form mechanischer Energie ist die potenzielle Energie. Die kinetische Energie kennzeichnet den Zustand eines sich bewegenden Körpers und wird deshalb wie jede Form von Energie auch als Zustandsgröße bezeichnet. Kinetische Energie kann in einem Körper gespeichert sein. Sie kann auch in andere Energieformen umgewandelt oder von einem Körper auf andere Körper übertragen werden.
Berechnung kinetischer Energie
Die kinetische Energie eines sich bewegenden Körpers hängt von seiner Masse bzw. seiner Geschwindigkeit ab. Sie ist umso größer,
- je größer die Masse des Körper ist und
- je größer seine Geschwindigkeit ist.
Die kinetische Energie eines sich bewegenden Körpers kann berechnet werden mit der Gleichung:
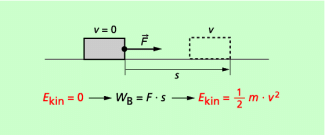
Sie ist genau so groß wie die Beschleunigungsarbeit, die erforderlich ist, um dem Körper die Geschwindigkeit v zu verleihen (Bild 2). Dabei ist zu beachten, dass sich die Geschwindigkeit v stets auf einen bestimmten Bezugskörper bzw. ein Bezugssystem bezieht. So hat z. B. eine Person, die in einem fahrenden Auto sitzt, gegenüber dem Bezugskörper Auto die kinetische Energie null, weil ihre Geschwindigkeit gegenüber dem Auto null ist. Gegenüber der Straße ist aber die kinetische Energie größer als null, da sich das Auto und damit auch die Person in ihm bezüglich der Straße mit einer bestimmten Geschwindigkeit bewegt.
Gerade bei Fahrzeugen ist zu beachten, dass die kinetische Energie mit dem Quadrat der Geschwindigkeit wächst. Das bedeutet: Eine Verdopplung der Geschwindigkeit eines Autos bedeutet eine Vervierfachung seiner kinetischen Energie. Das ist bei Unfällen von entscheidender Bedeutung.
Rotationsenergie
Auch rotierende Körper, z. B. sich drehende Schwungräder, ein rotierender Schleifstein oder ein rotierendes Karussell besitzen kinetische Energie, die auch als Rotationsenergie bezeichnet wird.
Die Rotationsenergie eines Körpers hängt ab von der Drehzahl und davon, wie sich die Masse des Körpers bezüglich der Drehachse verteilt. Sie ist umso größer,
- je größer die Drehzahl des Körpers ist,
- je größer seine Masse ist und
- je weiter die Masse von der Drehachse entfernt ist.
Schwungräder, in denen kinetische Energie gespeichert werden soll, baut man deshalb so, dass sie eine große Masse haben und sich der größte Teil der Masse relativ weit von der Drehachse entfernt befindet.
| Kinetische Energie in Natur und Technik | |
| Apfel (m = 100 g) nach 1 m freien Fall | 1 J |
| Fußgänger (m = 55 kg) bei 5 km/h | 50 J |
| Radfahrer (m = 75 kg) bei 20 km/h | 1 200 J |
| PKW (m = 1 000 kg) bei 50 km/h | 96 000 J = 96 kJ |
| PKW (m = 1 000 kg) bei 100 km/h | 386 000 J = 386 kJ |
| ICE (m = 500 t) bei 180 km/h | 625 MJ |
| Jumbo-Jet (m = 320 t) beim Abheben (310 km/h) | 1 200 MJ |
-

pdesign - Fotolia.com