Schräger Wurf
Unter einem schrägen Wurf versteht man die Überlagerung (Superposition) einer gleichförmigen Bewegung mit bestimmter Anfangsgeschwindigkeit (Abwurfgeschwindigkeit) schräg nach oben und des freien Falls.
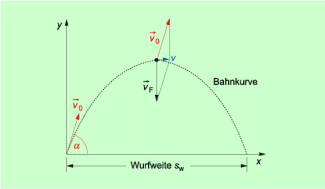
Die beiden Teilbewegungen ergeben eine resultierende (zusammengesetzte) Bewegung. Für diese resultierende Bewegung können Wege und Geschwindigkeiten rechnerisch oder zeichnerisch ermittelt werden. Dabei ist der vektorielle Charakter von Weg und Geschwindigkeit zu beachten.
Als Bahnkurve ergibt sich eine typische Wurfparabel.
Unter einem schrägen Wurf versteht man die Überlagerung (Superposition) einer gleichförmigen Bewegung mit bestimmter Anfangsgeschwindigkeit (Abwurfgeschwindigkeit) schräg nach oben und des freien Falls. Als Bahnkurve ergibt sich eine typische Wurfparabel. Für die Überlagerung von Bewegungen gilt das Unabhängigkeitsprinzip, das auch als Superpositionsprinzip bezeichnet wird. Es lautet:
Führt ein Körper gleichzeitig mehrere Teilbewegungen aus, so überlagern sich diese Teilbewegungen unabhängig voneinander zu einer resultierenden Gesamtbewegung.
Die Geschwindigkeiten bzw. die Wege addieren sich vektoriell (Bild 2). Für diese resultierende Bewegung können Geschwindigkeiten und Wege rechnerisch oder zeichnerisch ermittelt werden.
Für die resultierende Geschwindigkeit gilt:
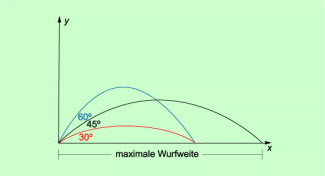
Von besonderem Interesse ist beim schrägen Wurf die Wurfweite (Bild 3). Sie hängt von der Anfangsgeschwindigkeit und vom Abwurfwinkel ab. Die größte Wurfweite wird bei einem Abwurfwinkel von 45° erreicht. Bei Winkeln, die sich zu 90° ergänzen, ist die Wurfweite gleich groß. So erreicht man z. B. bei einem Abwurfwinkel von 30° die gleiche Wurfweite wie bei einem Abwurfwinkel von 60°. Für die Wurfweite gilt:
Die größte Höhe, die ein Körper erreicht, wird als Wurfhöhe bezeichnet. Die Zeit bis zum Erreichen der größten Höhe ist die Steigzeit. Sie ist genau so groß wie die Fallzeit, also die Zeit zwischen dem Erreichen der größten Höhe und dem Auftreffen in Abwurfhöhe. Die Dauer des gesamten Wurfes ist also gleich der Summe aus Steigzeit und Fallzeit.
Wurfhöhe und Steigzeit können folgendermaßen berechnet werden:
Die Wege in horizontaler Richtung bzw. in vertikaler Richtung ergeben sich aus den Teilbewegungen und können folgendermaßen ermittelt werden:
Beachte: Die dargestellten Zusammenhänge gelten nur, wenn die vertikale Fallbewegung als freier Fall angenommen werden kann, wenn also der Luftwiderstand vernachlässigbar ist. Ist der Luftwiderstand nicht vernachlässigbar, dann entstehen keine Wurfparabeln, sondern ballistische Kurven. Unter diesem Stichwort sind dazu genauere Informationen zu finden.