Kurvendiskussion einer ganzrationalen Funktion
In den Natur- bzw. Technikwissenschaften versucht man, bestehende Sachverhalte mithilfe von Funktionen zu modellieren und zu beschreiben. Um die vorliegenden Zusammenhänge besser zu verstehen, ist es oft hilfreich, den Verlauf der entsprechenden Funktionsgraphen genauer zu untersuchen. Sofern keine Funktionsplotter zur Verfügung stehen, ist es notwendig, typische Eigenschaften der zu untersuchenden Funktion mithilfe geeigneter Methoden der Analysis zu bestimmen und den Funktionsgraphen danach zu zeichnen.
In der Regel sollte die Kurvendiskussion einer Funktion bzw. ihres Graphen nach der folgenden Schrittfolge durchgeführt werden:
- Bestimmen des größtmöglichen Definitionsbereiches
- Untersuchen auf Stetigkeit bzw. Unstetigkeit und Angabe eventueller Polstellen
- Untersuchen auf Symmetrieeigenschaften
- Untersuchen des Verhaltens im Unendlichen (Ermitteln der Asymptoten)
- Bestimmen der Nullstellen
- Ermitteln der Schnittpunkte mit der y-Achse
- Untersuchen auf lokale Extrempunkte
- Untersuchen auf Wendepunkte, ggf. auch Ermitteln der Wendetangenten
- Zeichnen des Graphen
Welche konkreten Überlegungen bei der Kurvendiskussion ganzrationaler Funktionen notwendig sind, soll an folgendem Beispiel verdeutlicht werden.
Gegeben sei die Funktion .
- Bestimmen des größtmöglichen Definitionsbereiches:
- Untersuchen auf Stetigkeit bzw. Unstetigkeit und Angabe eventueller Polstellen:
Ganzrationale Funktionen sind im gesamten Definitionsbereich stetig. - Untersuchen auf Symmetrieeigenschaften:
Die Funktion ist gerade.
Ihr Graph ist symmetrisch zur y-Achse. - Untersuchen des Verhaltens im Unendlichen:
- Bestimmen der Nullstellen:
Substitution liefert mit der Lösung
( entfällt)
Also gilt und damit
Die Funktion f hat die Nullstellen
Die Schnittpunkte mit der x-Achse lauten demnach . - Ermitteln der Schnittpunkte mit der y-Achse:
Da , hat der Funktionsgraph mit der y-Achse den Schnittpunkt . - Untersuchen auf lokale Extrempunkte:
Die Lösungen sind mögliche Extremstellen von f.
Nachweis der Extrema:
f hat an der Stelle ein lokales Maximum und an den Stellen lokale Minima: - Untersuchen auf Wendepunkte:
Die Lösungen sind mögliche Wendestellen.
Nachweis mithilfe der dritten Ableitung:
Der Graph von f hat die Wendepunkte
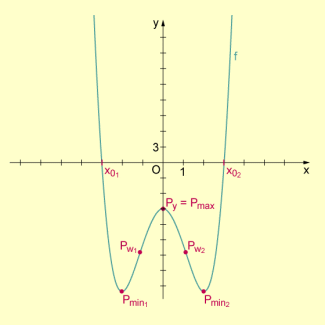
. - Grafische Darstellung :
-
Grafische Darstellung von f als Ergebnis einer Kurvendiskussion