- Lexikon
- Chemie Abitur
- 1 Die Chemie eine Naturwissenschaft
- 1.2 Denk- und Arbeitsweisen in der Chemie
- 1.2.2 Gesetze, Modelle und Theorien in der Chemie
- Gasgesetze und die Zustandsgleichung für ideale Gase (universelle Gasgleichung)
Gasgesetze und die Zustandsgleichung für ideale Gase (universelle Gasgleichung)
Zustandsgleichung für das ideale Gas
Um die Zusammenhänge zwischen Temperatur, Druck und Volumen von Gasen in einfacher Weise mathematisch beschreiben zu können, wird in der Naturwissenschaft häufig das Modell ideales Gas genutzt. Das ideale Gas als Modell ist wie jedes Modell eines Vereinfachung der Wirklichkeit.
Das Modell ideales Gas ist folgendermaßen gekennzeichnet:
- Die Teilchen des Gases werden als Punkte (Massepunkte) betrachtet, die zwar eine Masse, aber kein Volumen haben.
- Zwischen den Teilchen treten keine anziehenden und abstoßenden Kräfte auf.
- Die Stöße zwischen den Teilchen untereinander sowie zwischen den Teilchen und den Wänden des Gefäßes erfolgen vollkommen elastisch.
Veranschaulicht kann man sich das Modell ideales Gas durch sehr kleine, elastische Kugeln, die sich in einem abgeschlossenen Raum befinden.
Dieses Modell ist auf viele reale Gase wie Luft, Wasserstoff und alle Edelgase anwendbar, da zwischen den meisten Gasteilchen unter normalen Bedingungen nur schwache Wechselwirkungen auftreten.
Der Zusammenhang von Druck und Volumen in idealen Gasen
Die Luft in einem Wasserball oder in einer Luftmatratze hat bei einer bestimmten Temperatur ein bestimmtes Volumen und einen bestimmten Druck. Liegen ein solcher Ball oder eine Luftmatratze in der prallen Sonne, so verändert sich die Temperatur der Luft in ihnen. Damit ändern sich auch Volumen und Druck.
Bereits im 19. Jahrhundert erkannten die Naturwissenschaftler ROBERT BOYLE, EDME MARIOTTE und JOSEPH LOUISE GAY-LUSSAC, dass der Zustand eines Gases durch die drei Zustandsgrößen Druck, Volumen und Temperatur beschrieben werden kann. Sie untersuchten die Zusammenhänge zwischen den Zustandsgrößen und entdeckten die nach ihnen benannten Gesetzmäßigkeiten:
Das Gesetz von BOYLE und MARIOTTE
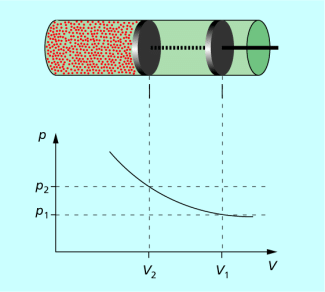
In einer Luftpumpe herrscht bei einem bestimmten Volumen der eingeschlossenen Luft ein bestimmter Druck. Wird der Kolben in den Zylinder hineingepresst, so verringert sich das Volumen. Der Druck vergrößert sich entsprechend (Bild 3). Es gilt:
Je kleiner das Volumen der eingeschlossenen Luft ist, desto größer ist der Druck in der Luft. |
Unter der Bedingung, dass die Temperatur in einem Gas konstant ist und sich das Gas wie das ideale Gas verhält, gilt:
Dieses Gesetz wurde erstmals 1662 von dem britischen Chemiker und Physiker ROBERT BOYLE (1627-1691) und, unabhängig davon, einige Jahre später von dem französischen Forscher EDME MARIOTTE (um 1620-1684) formuliert und wird heute als Gesetz von BOYLE und MARIOTTE oder auch als Druck-Volumen-Gesetz bezeichnet. Da bei dem betrachteten Vorgang die Temperatur des Gases konstant bleibt, sich aber Druck und Volumen ändern, spricht man in der Physik auch von einer isothermen Zustandsänderung des Gases.
Beispiele für das Wirken des Gesetzes
Beispiele für das Wirken des Gesetzes von BOYLE und MARIOTTE treten überall dort auf, wo sich das Volumen abgeschlossener Gasmengen ändert und dabei die Temperatur näherungsweise konstant ist.
Beispiele dafür sind Luftpumpen oder Pumpen für Sauerstoff in der Medizin. Auch bei Wasserbällen oder Luftmatratzen zeigt sich der Zusammenhang zwischen Druck und Volumen: Je mehr Luft man hineinbläst, desto größer wird der Druck. Mit Vergrößerung des Druckes vergrößert sich auch das Volumen.
Das Gesetz von GAY-LUSSAC
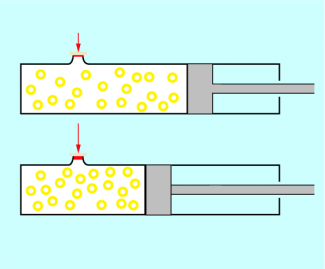
In einem abgeschlossenen Wohn- oder Arbeitsraum herrscht der jeweilige Luftdruck, der sich nur in geringen Grenzen verändert. Bei einer bestimmten Temperatur hat die Luft im Raum ein bestimmtes Volumen. Wenn sich die Temperatur der Luft ändert, z. B. beim Aufdrehen der Heizung, ändert sich auch das Volumen der Luftmenge, die ursprünglich in Raum war. Da sich der Raum nicht vergrößert, strömt ein Teil der Luft aus bzw. bei Verringerung der Temperatur in den Raum hinein.
Je höher die Temperatur ist, desto größer ist bei einem bestimmten Druck das Volumen, das eine bestimmte Gasmenge einnimmt. |
Unter der Bedingung, dass der Druck in einem Gas konstant ist und sich das Gas wie das ideale Gas verhält, gilt:
Das Gesetz wurde erstmals 1802 von dem französischen Chemiker und Physiker JOESPH LOUIS GAY-LUSSAC (1778-1850) formuliert und wird heute als Gesetz von GAY-LUSSAC oder auch als Volumen-Temperatur- Gesetz bezeichnet. Da bei dem betrachteten Vorgang der Druck des Gases konstant bleibt, sich aber bei Erwärmung Temperatur und Volumen ändern, spricht man in der Physik auch von einer isobaren Zustandsänderung des Gases.
Durch Volumenverringerung erhöht sich der Druck des Gases in der Luftpumpe.
Beispiele für das Wirken des Gesetzes
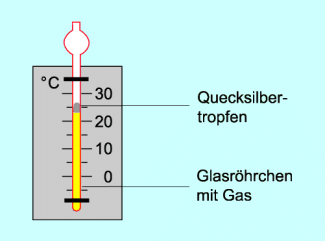
Beispiele für das Wirken des Gesetzes von GAY-LUSSAC sind Gasthermometer (Bild 4) oder Räume und Gefäße, in denen näherungsweise ein konstanter Druck herrscht und bei denen sich die Temperatur des eingeschlossenen Gases ändert.
Bei Wohnräumen ist der Druck gleich dem Luftdruck. Bei einer bestimmten Temperatur befindet sich in einem solchen Raum eine bestimmte Menge Luft. Wird durch Heizen die Temperatur erhöht, so nimmt die Luftmenge ein größeres Volumen ein. Da sich die Raumgröße nicht ändert, strömt ein Teil der Luft aus. Umgekehrt verringert sich bei Verringerung der Temperatur das Volumen einer bestimmten Gasmenge. In einen Raum würde dann von außen Luft einströmen.
Spezielle Zustandsänderungen idealer Gase
Die Gesetze von GAY-LUSSAC beschreibt die isobare (p = konstant) und das Gesetz von BOYLE und MARIOTTE die isotherme Zustandsänderung (T = konstant) idealer Gase. Ein dritter Spezialfall tritt auf, wenn bei einem konstanten Volumen eines Gases die Temperatur verändert wird. Erhitzt man beispielsweise einen geschlossenen Schnellkochtopf oder einen chemischen Reaktor, dann steigt der Druck. Diese isochore Zustandänderung wird durch das Gesetz von AMONTONS quantitativ beschrieben.
In vielen Fällen sind jedoch alle drei Zustandsgrößen Druck, Volumen und Temperatur eines Gases veränderbar. Die Änderung hängt auch davon ab, wie viel Gasmoleküle sich in einem bestimmten Volumen befinden und damit von der Stoffmenge des idealen Gases. Je größer die Stoffmenge des Gases, desto größer ist die beobachtete Druck- und Volumenzunahme bei einer Temperaturerhöhung.
Fasst man die drei Gasgesetze zusammen und bezieht die Stoffmenge in die Betrachtungen mit ein, erhält man folgenden Ausdruck:
Dieser Quotient ergibt für ideale Gase unabhängig von den Bedingungen den gleichen konstanten Wert R, den man als universelle Gaskonstante R bezeichnet. Durch Einsetzen von R und Umstellen erhält man die Zustandsgleichung für das ideale Gas, die auch universelle Gasgleichung genannt wird. Man findet auch die Bezeichnungen allgemeine Zustandsgleichung für das ideale Gas oder ideale Gasgleichung.
Aufbau eines Gasthermometers
Für ein reales Gas ist die Zustandsgleichung anwendbar, wenn sich dieses näherungsweise wie das ideale Gas verhält. Diese Bedingung erfüllen eine Vielzahl realer Gase wie Luft, Sauerstoff oder Stickstoff.
Dadurch bedingt kann die universelle Gasgleichung für viele Berechnungen genutzt werden. Besondere Bedeutung hat sie in der Stöchiometrie, weil man aus dem Volumen, dem Druck und der Temperatur sehr leicht die Stoffmenge und daraus die Masse von Gasen in chemischen Reaktionen ermitteln kann (Rechenbeispiel).
Material zum Thema
Gesetz Zusammenhang zwischen Druck und Volumen Zustandsgleichung für das ideale Gas Gay-Lussac Gasthermometer Mariotte Boyle Rechenbeispiel Zustandsgrößen ideales Gas^ Gasgesetze Temperatur
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 