Areafunktionen (inverse Hyperbelfunktionen)

Da die hyperbolischen Funktionen über ihrem Definitionsbereich (bzw. über einem Teilbereich von diesem) monoton sind, existieren ihre Umkehrfunktionen. Diese werden als Areafunktionen bezeichnet. Sie lassen sich mithilfe des natürlichen Logarithmus darstellen.

Funktion	Umkehrfunktion
$y = \sinh x (x \in ℝ)$	$y = a r \sinh x (x \in ℝ)$ (Sprechweise: area sinus hyperbolicus x)
$y = \cosh x (x \in ℝ; x \geq 0)$	$y = a r \cosh x (x \geq 1)$
$y = \tanh x (x \in ℝ)$	$y = a r \tanh x (- 1 < x < 1)$
$y = \coth x (x \in ℝ; x \neq 0)$	$y = a r \coth x (\| x \| > 1)$

Für die Areafunktionen lassen sich explizite Darstellungen unter Verwendung des natürlichen Logarithmus angeben. Im Folgenden wird eine solche Darstellung am Beispiel der Umkehrung der Funktion $y = \sinh x$ entwickelt.

Es gilt $y = a r \sinh x$ genau dann, wenn $x = \sinh y = \frac{1}{2} (e^{y} - e^{- y})$ ist, d.h.:
$2 x = e^{y} - e^{- y} b z w . e^{y} - 2 x - \frac{1}{e^{y}} = 0 b z w . e^{2 y} - 2 x e^{y} - 1 = 0$

Diese Gleichung lässt sich als quadratische Gleichung in $e^{y}$ auffassen, deren Lösungen $x \pm \sqrt{x^{2} + 1}$ sind. Da $e^{y}$ nicht negativ wird, kann nur die Lösung $e^{y} = x + \sqrt{x^{2} + 1}$ gewählt werden. Somit ist:
$y = a r \sinh x = \ln (x + \sqrt{x^{2} + 1})$

Entsprechend erhält man für die anderen Areafunktionen die folgenden Darstellungen:
$\begin{array}{l} y = a r \cosh x = \ln (x + \sqrt{x^{2} - 1}) (x \in [1; \infty [) \\ y = a r \tanh x = \frac{1}{2} \ln \frac{1 + x}{1 - x} (| x | < 1) \\ y = a r \coth x = \frac{1}{2} \ln \frac{x + 1}{x - 1} (| x | > 1) \end{array}$

Die Bilder der Areafunktionen ergeben sich aus denen der hyperbolischen Funktionen durch Spiegelung an der Geraden $y = x$ .

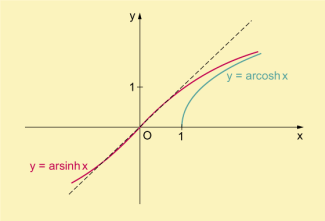
Umkehrfunktionen des Hyperbelsinus und Hyperbelkosinus

In der folgenden Übersicht sind einige Eigenschaften der Areafunktionen zusammengestellt (die sich aus den entsprechenden Eigenschaften des natürlichen Logarithmus ableiten).

Bild

Die Bezeichnung Areafunktion resultiert aus der geometrischen Deutung als Flächeninhalt des Sektors einer gleichseitigen Hyperbel (d.h. einer Hyperbel mit der Gleichung $x^{2} - y^{2} = 1$ ):

Bild

Hier gilt: $A_{1} = \frac{1}{2} a r \cosh a$
Das lässt sich wie folgt zeigen:
$A_{1} = A_{O Q P} - A_{2} m i t Q (a; 0)$
$A_{O Q P} = \frac{1}{2} a \sqrt{a^{2} - 1}; A_{2} = \int_{1}^{a} \sqrt{x^{2} - 1} d x$
Die Berechnung von $\int_{1}^{a} \sqrt{x^{2} - 1} d x$
(mittels Substitution $x = \cosh z$ und anschließender partieller Integration) ergibt:
$\int_{1}^{a} \sqrt{x^{2} - 1} d x = \frac{1}{2} a \sqrt{a^{2} - 1} - \frac{1}{2} a r \cosh a$
Daraus folgt:
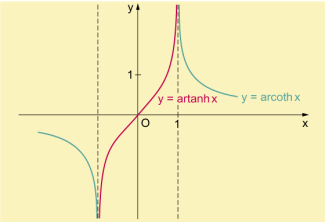
$A_{1} = \frac{1}{2} a \sqrt{a^{2} - 1} - (\frac{1}{2} a \sqrt{a^{2} - 1} - \frac{1}{2} a r \cosh a) = \frac{1}{2} a r \cosh a$

Umkehrfunktionen des Hyperbeltangens und Hyperbelkotangens

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Areafunktionen (inverse Hyperbelfunktionen)

Rechtliches

Einloggen