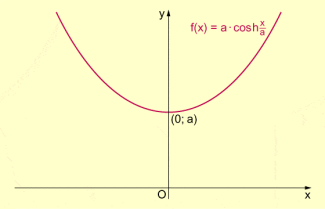
Die Kettenlinie

Unter dem Einfluss ihres Eigengewichtes nimmt eine Kette (oder ein Seil) bei Aufhängung an zwei nicht übereinanderliegenden Punkten bei Ruhe die Form einer Kettenlinie an. Diese hängt von der Lage der Aufhängepunkte und der Länge der Kette, nicht jedoch von ihrem Gewicht pro Längeneinheit ab.

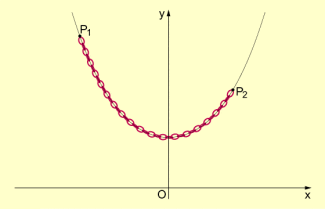
Das Problem der Kettenlinie wurde erstmals von GALILEO GALILEI (1564 bis 1642) untersucht. Es geht dabei um folgende Frage:

• Welche Kurve nimmt eine an ihren Enden aufgehängte Kette ein?
  (Möglicherweise hat dieses Problem sogar eine praktische Bedeutung; man denke etwa an die Konstruktion von Hängebrücken.)

GALILEI glaubte, dass die Kettenlinie eine Parabel sei. Diese Annahme wurde vom deutschen Mathematiker, Physiker und Philosophen JOACHIM JUNGIUS (1587 bis 1657) in seiner 1639 erschienenen „Geometria empyrica“ widerlegt.

Auch CHRISTIAAN HUYGENS (1629 bis 1695) wies den Fehler GALILEIS bei der Lösung nach, indem er zeigte, dass die Kettenlinie keine Parabel sein könne (und dies, wo doch selbst die päpstlichen Inquisition keinen Fehler im Werk GALILEIS gefunden hatte).

Mit dem Problem der Kettenlinie beschäftigten sich auch die Brüder JAKOB BERNOULLI (1654 bis 1705) und JOHANN BERNOULLI (1667 bis 1748) sowie der deutsche Gelehrte GOTTFRIED WILHELM LEIBNIZ (1646 bis 1716). Eine Lösung, d.h. die explizite Herleitung einer diese Funktion beschreibenden Gleichung, gelang im Jahre 1690.

Die Art und Weise, wie man heute dieses Problem angeht, sei im Folgenden skizziert (sie entspricht etwa dem Weg, den JOHANN BERNOULLI seinerzeit gegangen ist).

Die Kraft, die eine Kette spannt, ist ihr eigenes Gewicht G. Da die Kette im Gleichgewicht ist, sind die Kraftkomponenten in x-Richtung gleich, d.h., es ist $F_1^x=F_2^x=c$.

Es gilt:
$f\text{'}(x_1)=\frac{F_1^y}{F_1^x}=\frac{F_1^y}{c}bzw.f\text{'}(x_2)=\frac{F_2^y}{F_2^x}=\frac{F_2^y}{c}$

Damit ergibt sich:
$F_1^y=f\text{'}(x_1)\cdot cund{F}_2^y=f\text{'}(x_2)\cdot c$

Allgemein findet man für $x_1=x$ und $x_2=x+dx$ (vgl. die einleitende Bemerkung):
$F(x+dx)-F(x)=G$

Bezeichnet H den als konstant angenommenen Durchmesser der Kette, $\gamma$ das spezifische Gewicht des Materials und ds das Bogenelement, so lässt sich das Gewicht G des Kettenstücks zwischen x und $x+dx$ schreiben als
$G=\gamma \cdot H\cdot ds=\gamma \cdot H\cdot \left(\sqrt{1+{\left[f\text{'}(x\right]}^2}dx\right)$.

Insgesamt findet man:
$\begin{array}{l}c\cdot \left[f\text{'}(x+dx)-f\text{'}(x)\right]=\gamma \cdot H\cdot \sqrt{1+{\left[f\text{'}(x\right]}^2}dx\\ c\cdot \frac{f\text{'}(x+dx)-f\text{'}(x)}{dx}=\gamma \cdot H\cdot \sqrt{1+{\left[f\text{'}(x\right]}^2}\\ c\cdot f\text{'}\text{'}(x)=\gamma \cdot H\cdot \sqrt{1+{\left[f\text{'}(x\right]}^2}\\ \frac{f\text{'}\text{'}(x)}{\sqrt{1+{\left[f\text{'}(x\right]}^2}}=\frac{\gamma \cdot H}{c}\end{array}$

Das ist die Differenzialgleichung der Kettenlinie in moderner Schreibweise. Die BERNOULLIS benutzten eine Integralform dieser Gleichung, nämlich $\frac{dy}{dx}=\frac{\gamma \cdot H}{c}\cdot s$.

Die Lösung ist
$\frac{a}{2}\cdot \left(e^{\frac{x}{a}}+e^{-\frac{x}{a}}\right)=a\cdot \cosh \left(\frac{x}{a}\right)mita=\frac{c}{\gamma \cdot H}$,
also die sogenannte Kettenlinie (oder der Cosinus hyperbolicus).