Bedingte Wahrscheinlichkeit
Der Grad der Gewissheit über das Eintreten eines zufälligen Ereignisses A wird durch seine Wahrscheinlichkeit angegeben.
Liegt jedoch die Information über das Eintreten eines Ereignisses B vor, so kann diese die Bewertung der Eintrittschancen von A verändern, was durch die bedingte Wahrscheinlichkeit beschrieben wird.
-
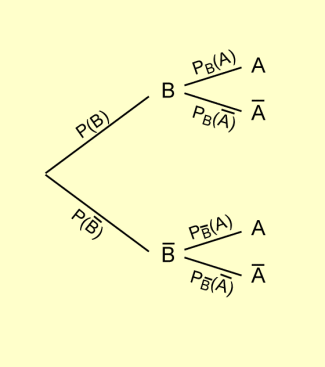
Bedingte Wahrscheinlichkeiten als Übergangswahrscheinlichkeiten im Baumdiagramm
- Als bedingte Wahrscheinlichkeit des Ereignisses A unter der Bedingung B bezeichnet man , falls gilt.
Anmerkung: Für die bedingte Wahrscheinlichkeit ist auch die Schreibweise üblich. Diese ältere einzeilige Schreibweise ist schreibtechnisch zwar vorteilhafter als , aber bei der Schreibweise wird die im Vergleich zu P veränderte Wahrscheinlichkeitsfunktion stärker hervorgehoben.
-
Faires Tetraeder
- Beispiel: Zweimaliges Werfen eines fairen Tetraeders
Das Ereignis
hat die Wahrscheinlichkeit .
Sei B nun das Ereignis
so gilt .
Folglich ergibt sich:
Jede bedingte Wahrscheinlichkeitsverteilung ist wie P eine Wahrscheinlichkeitsverteilung, die auch den drei kolmogorowschen Axiomen genügt. Folglich gelten für dieselben Rechenregeln wie für P, z.B. und .
Jede „unbedingte“ Wahrscheinlichkeit kann als bedingte Wahrscheinlichkeit aufgefasst werden, nämlich als Wahrscheinlichkeit des Ereignisses A unter der Bedingung des sicheren Ereignisses , d.h. , weil gilt.
Um bedingte Wahrscheinlichkeiten zu berechnen, verwendet man außer ihrer Definition und ihren Rechenregeln häufig als praktische Hilfsmittel Baumdiagramme oder Vierfeldertafeln.
Im Baumdiagramm stellen sich die bedingten Wahrscheinlichkeiten entsprechend der ersten Pfadregel als Übergangswahrscheinlichkeiten dar (in der folgenden Abbildung links). Um auch die „umgekehrte“ bedingte Wahrscheinlichkeit als Übergangswahrscheinlichkeit aus einem Baumdiagramm direkt abzulesen, benötigt man das „umgekehrte“ Baumdiagramm (in der folgenden Abbildung rechts).
![]()
In den Mengendiagrammen Vierfeldertafel und VENN-Diagramm ist als der Anteil von A zu interpretieren, der in B liegt, d.h. als das Verhältnis des Flächenmaßes von zum Flächenmaß von B, also .
![]()
lässt sich auf diese Weise als der Anteil von A interpretieren, der in liegt. Da dies jedoch das gesamte A ist (es gilt ), erhält man .
Stimmt für zwei Ereignisse A und B die bedingte Wahrscheinlichkeit mit der (unbedingten) Wahrscheinlichkeit überein, so sind A und B unabhängig voneinander.

