Der Multiplikationssatz für Ereignisse

In der Praxis steht man oftmals vor der Notwendigkeit, Wahrscheinlichkeiten für Ereignisse der Gestalt $A \cap B$ zu berechnen. Dies erweist sich aber nicht immer als ganz einfach. Wir betrachten dazu zwei Anwendungsbeispiele.

Beispiel 1: Um die Frage beantworten zu können, mit welcher Wahrscheinlichkeit bei 17-jährigen Jungen Diabetes auftritt, sollen 1000 rein zufällig ausgewählte männliche Personen im Alter von 17 Jahren gezielt untersucht werden. Dabei ist beabsichtigt, zwei Diagnoseverfahren $D_{1}$ und $D_{2}$ einzusetzen.

Während das Verfahren $D_{1}$ einfach handhabbar und kostengünstig ist, belastet $D_{2}$ den Probanden erheblich und verursacht deutlich mehr Kosten als $D_{1}$ . Die untersuchte Person hat aber nur dann Diabetes, wenn sowohl $D_{1}$ als auch $D_{2}$ einen positiven Befund ergeben haben.
(Es soll hier unberücksichtigt bleiben, dass die Ergebnisse derartiger Diagnoseverfahren in der Praxis selbst mit einer gewissen Fehlerwahrscheinlichkeit behaftet sind.)

Anstatt alle 1000 Testpersonen mittels der Verfahren $D_{1}$ und $D_{2}$ zu untersuchen, wäre es günstiger, zuerst bei allen Probanden $D_{1}$ anzuwenden und $D_{2}$ dann nur bei jenen, bei denen $D_{1}$ einen positiven Befund $(D_{1}^{+})$ ergeben hat.

Aber wie lässt sich dann eine Wahrscheinlichkeitsaussage über das relevante Ereignis $D_{1}^{+} \cap D_{2}^{+}$ machen?

Wir betrachten dazu den allgemeinen Multiplikationssatz (Produktsatz) für zwei Ereignisse:

Sind A, B zwei Ereignisse eines Zufallsexperiments mit $P (B) > 0$ , so gilt:
$P (A \cap B) = P (B) \cdot P_{B} (A)$

Bezüglich dieses Multiplikationssatzes stellen wir fest:

Der Satz entspricht der ersten Pfadregel im zweistufigen Baumdiagramm (siehe auch die folgende Abbildung).
Der Satz ist eine Produktform der definierenden Gleichung für bedingte Wahrscheinlichkeiten:
$P_{B} (A) = \frac{P (A \cap B)}{P (B)} f ü r P (B) > 0$

Allgemeiner Multiplikationssatz für zwei Ereignisse im Baumdiagramm

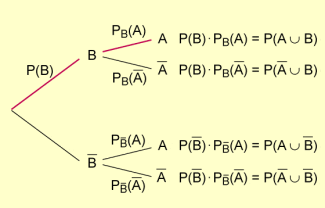
Kehren wir zu unserem Eingangsbeispiel zurück. Nimmt man fiktiv an, dass bei 290 Probanden das Verfahren $D_{1}$ einen positiven Befund ergeben hat und dass bei 35 von diesen 290 auch $D_{2}$ positiv war, so ergibt sich (wenn man für die betreffenden Wahrscheinlichkeiten näherungsweise die relativen Häufigkeiten verwendet):
$P (D_{1}^{+} \cap D_{2}^{+}) = P (D_{1}^{+}) \cdot P_{D_{1}^{+}} (D_{2}^{+}) = 0,29 \cdot \frac{35}{290} = 0,035 \approx 0,04$

Das Beispiel verdeutlicht auch die Erfahrung aus der Praxis, dass für Berechnungen häufig nicht die Formel für $P_{B} (A)$ , sondern der gleichwertige Multiplikationssatz zur Berechnung von $P (A \cap B)$ verwendet wird.

Verallgemeinerung des Multiplikationssatzes für n Ereignisse
Der allgemeine Multiplikationssatz (Produktsatz) für zwei Ereignisse lässt sich wie folgt für n Ereignisse $A_{1}, A_{2}, ..., A_{n}$ verallgemeinern:

Sind $A_{1}, A_{2}, ..., A_{n}$ n Ereignisse eines Zufallsexperiments mit $P (A_{1} \cap A_{2} \cap ... \cap A_{n - 1}) > 0$ , so gilt:
$P (A_{1} \cap A_{2} \cap ... \cap A_{n}) = P (A_{1}) \cdot P_{A_{1}} (A_{2}) \cdot P_{A_{1} \cap A_{2}} (A_{3}) \cdot ... \cdot P_{A_{1} \cap ... \cap A_{n - 1}} (A_{n})$

Diesen Multiplikationssatz kann man sich gut an einem n-stufigen Vorgang veranschaulichen.

Allgemeiner Multiplikationssatz für n Ereignisse im Baumdiagramm

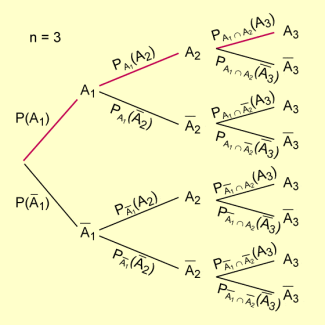
Das Ereignis $A_{1} \cap A_{2} \cap ... \cap A_{n}$ kann gleichsam schrittweise entlang eines Pfades im n-Stufigen Baumdiagramm abgearbeitet werden:

Als Erstes tritt $A_{1}$ mit $P (A_{1})$ ein.
Unter der Bedingung, dass $A_{1}$ eingetreten ist, tritt $A_{2}$ mit der Wahrscheinlichkeit $P_{A_{1}} (A_{2})$ ein.
Unter der Bedingung, dass $A_{1} \cap A_{2}$ eingetreten sind, tritt $A_{3}$ mit der Wahrscheinlichkeit $P_{A_{1} \cap A_{2}} (A_{3})$ ein usw.

Wir betrachten auch zum Multiplikationssatz für mehr als zwei Ereignisse ein Beispiel:

Beispiel 2: Jonas, Lars und Karin möchten mit ihren bunten Glaskugeln Murmeln spielen. Sie können sich nicht einigen, wer beginnt. Karin schlägt vor, dass aus ihrem Säckchen, in dem sich genau $n = 7$ Kugeln, davon $g = 5$ grüne und $n - g = 2$ weiße Kugeln, befinden, jeder von ihnen dem Alter nach (der Jüngste beginnt) eine Kugel zieht. Wer als Erster eine grüne Kugel zieht, der darf beim Murmelspiel beginnen.

Lars protestiert, da Jonas als der Jüngste bevorteilt sei. Karin versucht Lars zu beruhigen, indem sie darauf verweist, dass die gezogene Kugel nicht zurückgelegt wird und dass damit die Gewinnchancen von Lars, der als Zweiter zieht, wachsen müssten. „Und vielleicht ist meine Gewinnchance sogar am größten, denn wenn ich als Dritte zum Ziehen komme, befinden sich nur noch grüne Kugeln im Säckchen“, sagt Karin.

Es sei $z_{i}$ das Ergebnis der i-ten Ziehung mit $z_{i} \in {g r ü n; w e i ß}$ und $i = 1; 2; 3.$

Baumdiagramm zum Beispiel „Murmelspiel“

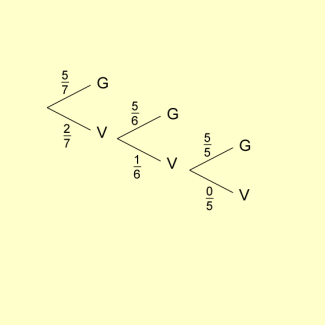
Dann gilt:
$P ({J o n a s g e w i n n t}) = P ({z_{1} = g r ü n}) = \frac{5}{7} \approx 0,71$

$\begin{array}{l} P ({L a r s g e w i n n t}) = P ({z_{1} = w e i ß} \cap {z_{2} = g r ü n}) \\ = P ({z_{1} = w e i ß}) \cdot P_{{z_{1} = w e i ß}} ({z_{2} = g r ü n}) \\ = \frac{2}{7} \cdot \frac{5}{6} = \frac{5}{21} \approx 0,24 \end{array}$
$\begin{array}{l} P ({K a r i n g e w i n n t}) = P ({z_{1} = w e i ß} \cap {z_{2} = w e i ß} \cap {z_{3} = g r ü n}) \\ = P ({z_{1} = w e i ß}) \cdot P_{{z_{1} = w e i ß}} ({z_{2} = w e i ß}) \cdot \\ \cdot P_{{z_{1} = w e i ß} \cap {z_{2} = w e i ß}} ({z_{3} = g r ü n}) \\ = \frac{2}{7} \cdot \frac{1}{6} \cdot \frac{5}{5} = \frac{1}{21} \approx 0,05 \end{array}$

Die Vermutung von Lars hat sich folglich als richtig erwiesen. Da Jonas zuerst ziehen durfte, hat er die größte Gewinnchance.

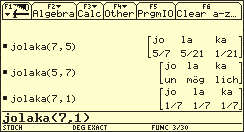
Es kann auch interaktiv untersucht werden, ob es möglich ist, die Werte für n und g so zu wählen, dass der Vorteil der ersten Ziehung hinsichtlich der Gewinnchancen der Nachziehenden ausgeglichen werden kann, wie die folgenden Abbildungen zeigen.

Drei mögliche Werte der Funktion „ jolaka“

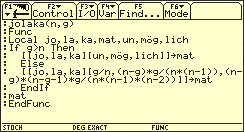
Definition der Funktion „jolaka“ (zum Berechnen der drei Gewinnahrscheinlichkeiten für Jonas, Lars und Karin (Beispiel mit Variablen n und g)

Wird in obigem Beispiel die gezogene Kugel allerdings wieder zurückgelegt, dann würden die Chancen für den Nachziehenden, eine grüne Kugel zu ziehen, gleich bleiben, d.h. es würde gelten:
$P_{{z_{1} = w e i ß}} ({z_{2} = g r ü n}) = P ({z_{2} = g r ü n})$
und
$P ({z_{1} = w e i ß} \cap {z_{2} = g r ü n}) = P ({z_{1} = w e i ß}) \cdot P ({z_{2} = g r ü n})$

Die Information, dass Jonas eine weiße Kugel gezogen hat, bringt Lars in diesem Fall auch keine erhöhte Chance, eine grüne Kugel zu ziehen. Dies bedeutet, es liegt stochastische Unabhängigkeit vor.

Für n voneinander (vollständig) unabhängige Ereignisse vereinfacht sich der Multiplikationssatz zu folgender Aussage (spezieller Multiplikationssatz):
$P (A_{1} \cap A_{2} \cap ... \cap A_{n}) = P (A_{1}) \cdot P (A_{2}) \cdot ... \cdot P (A_{n})$

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Angaben zum Lexikon

Impressum

Der Multiplikationssatz für Ereignisse

Rechtliches

Einloggen