Bonaventura Cavalieri
Leben und Wirken
Das Geburtsjahr von BONAVENTURA FRANCESCO CAVALIERI ist nicht verbürgt. Wahrscheinlich wurde er im Jahre 1598 geboren (einige Quellen nennen auch das Jahr 1591).
Im Jahre 1616 trat CAVALIERI in den Jesuitenorden ein – in jener Zeit typisch für junge Leute, die nach guter Bildung strebten. Hier setzte er als Autodidakt seine (etwa ab 1614 begonnene) Beschäftigung mit der Mathematik fort. Aufgrund seiner dabei erzielten Erfolge übertrug man ihm 1619 vertretungsweise eine Professur in Pisa.
Von 1620 bis 1623 wirkte CAVALIERI im Auftrag des Jesuitenordens in Mailand, anschließend war er Prior (Klostervorsteher) zunächst in Lodi und dann in Parma. Ab 1629 wirkte er in Bologna, wo er am 30. November 1647 (mitunter wird auch der 3. Dezember 1647 genannt) verstarb.
Zu wissenschaftlichen Leistungen
CAVALIERI veröffentlichte seine Arbeiten sehr spät. 1632 erschien als erste seiner Abhandlungen „Lo speccio ustorio“ – eine Arbeit zur Mechanik, u.a. zum Problem der Falllinie. Intensiv beschäftigte sich CAVALIERI mit trigonometrischen Problemen. Zu nennen sind hier das Buch „Directorium Generale Uranometricum“, in dem als wichtigstes Ergebnis der Flächeninhalt sphärischer Dreiecke angegeben wird, sowie die 1643 erschienene Tabellensammlung zur Trigonometrie („Trigonometria plana“).
Das Hauptwerk CAVALIERIS ist jedoch seine 1635 veröffentlichte „Geometria indivisibilibus continuorum nava quadam ratione promata“. Hierin berechnet er u.a. Flächeninhalte und Volumina nach der Methode der Indivisiblen.
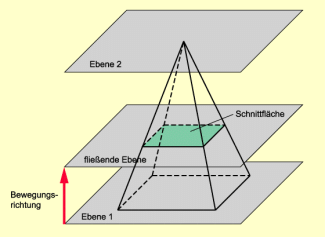
Unter Indivisiblen stellte er sich unendlich kleine, unteilbare Schichten eines Körpers oder einer Fläche vor. Sie entstehen nach seiner Auffassung auf folgende Weise: Jeder Körper kann zwischen zwei zueinander parallele Ebenen gelegt werden, die ihn in einem Punkt oder einer Begrenzungsfläche berühren. Wenn sich jetzt die eine Ebene parallel zu ihrer Ausgangslage zur anderen Ebene hin bewegt (CAVALIERI bezeichnet dies als „Fließen“), entstehen unendlich viele Schnittflächen der Ebene mit dem Körper. Der Körper ist dann die Gesamtheit dieser Schnittflächen.
CAVALIERI versuchte, mit diesem Ansatz das Problem der unendlich kleinen Größen zu erfassen, das die Mathematiker seit der Antike bewegte. Bei der weiteren Entwicklung der Mathematik zeigte sich aber, dass diese anschauliche Vorstellung von unendlich kleinen Größen zu zahlreichen logischen Widersprüchen führt. Deshalb musste man sich wieder davon lösen. Die Auffassungen CAVALIERIS führten jedoch zu zahlreichen richtigen Erkenntnissen und hatten starken Einfluss auf die Erarbeitung von Methoden zur Bestimmung von Flächen- und Rauminhalten.
Insbesondere gelangte CAVALIERI zu der heute als cavalierisches Prinzip (bzw. Satz des CAVALIERI) bezeichneten Aussage. Diese besagt, dass zwei Körper volumengleich sind, wenn sie in Grundfläche und Höhe übereinstimmen sowie alle zur Grundfläche parallelen Schnittflächen inhaltsgleich sind. CAVALIERI hat das nicht bewiesen, sondern als Prinzip bei Flächen- und Volumenberechnungen verwendet. Die Gültigkeit jenes Prinzips wurde zu Lebzeiten CAVALIERIS stark angezweifelt, so u.a. vom Jesuiten PAUL GULDIN (der Inhaltsberechnungen anhand von Schwerpunktbetrachtungen durchführte).
Ein exakter Beweis des cavalierischen Prinzips war erst mit den Mitteln der Infinitesimalrechnung möglich.
Prinzip der Flächen- und Volumenberechnung nach Cavalieri
Körper Ebenenschnitte Indivisiblen Satz des Cavalieri cavalierisches Prinzip Guldin> Paul Volumen Rauminhalt Cavalieri
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 