Das Geburtstagsproblem
Sarah ist stolz darauf, dass sie am gleichen Tag wie ihr Lieblingsonkel Lutz Geburtstag hat. Das ist für sie Ausdruck einer besonderen Fügung des Schicksals. Etwas enttäuscht ist sie allerdings, als ihr Onkel meint, es sei nicht so außergewöhnlich, dass von den insgesamt 32 lebenden Mitgliedern ihrer Familie zwei am gleichen Tag Geburtstag haben.
Um die Aussage des Onkels zu überprüfen, muss man sich etwas näher mit dem sogenannten Geburtstagsproblem beschäftigen, das auf den österreichischen Mathematiker RICHARD VON MISES (1883 bis 1953) zurückgeht.
Als Geburtstagsproblem wird die folgende Aufgabe bezeichnet:
- Wie groß ist die Wahrscheinlichkeit für das Ereignis , dass von n Personen mindestens zwei am gleichen Tage Geburtstag haben?
Für die Lösung dieser Aufgabe lassen wir uns von drei Modellannahmen leiten.
- Annahme 1: Jedes Jahr habe einheitlich 365 Tage, d.h., Schaltjahre werden ignoriert.
Diese Annahme wird zu einer geringfügig größeren Wahrscheinlichkeit als der tatsächlichen führen. - Annahme 2: Alle 365 Tage eines Jahres sind als Geburtstage gleichwahrscheinlich.
Diese nahe liegende Annahme ist in der Realität nicht erfüllt. Sie wird zu einer etwas kleineren Wahrscheinlichkeit als der tatsächlichen führen. - Annahme 3: Die Auswahl der n Personen erfolgt hinsichtlich ihres Geburtstages „auf gut Glück“.
Mit diesen Annahmen kann man das Geburtstagsproblem mathematisch fassen, wobei im Interesse einer vereinfachenden Schreibweise die Tage des Jahres von 1 bis 365 durchnummeriert werden. Dann ist:
(Sind mindestens zwei Geburtstage gleich, so gilt .
Wenn alle Geburtstage verschieden sind, so ist .)
Gesucht wird für , insbesondere für n = 32.
Lösungsvariante 1 (Statistische Erhebung)
Eine Lösungsmöglichkeit besteht darin, eine statistische Erhebung durchzuführen.
Indem man zum Beispiel die Schüler der eigenen Schule befragt, kann man eine größere Anzahl von Geburtsdaten ermitteln, die unter Berücksichtigung der Annahme 3 in k Gruppen bestehend aus n = 32 Geburtstagen eingeteilt werden. So ist es möglich, die relative Häufigkeit für das Ereignis zu ermitteln. Für große Werte von k kann die relative Häufigkeit entsprechend dem empirischen Gesetz der großen Zahlen als gute Näherung für die gesuchte Wahrscheinlichkeit angesehen werden. Vorteilhaft bei diesem Ansatz ist, dass Annahmen 1 und 2 nicht benötigt werden. Andererseits ist es in der Praxis nicht ganz einfach, die erforderliche Datenmenge zu bekommen. So müssten etwa für und n = 32 insgesamt 3200 Geburtstage unter Berücksichtigung der Annahme 3 erfragt werden.
-
Sortierte Liste von 32 zufälligen Geburtstagen
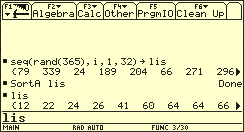
-
Simulation des Geburtstagsproblems
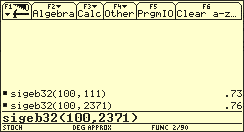
Lösungsvariante 2 (Simulation)
Die vorangehenden Abbildungen zeigt, wie durch Simulation eine aufsteigend sortierte Liste von 32 zufälligen Geburtstagen erzeugt werden kann. Wenn man diese erste Liste nach gleichen Elementen durchsucht und den Simulationsvorgang 100-mal wiederholt, lässt sich errechnen. Rechentechnisch weniger aufwendig kann man die Simulation mit der programmierten Funktion durchführen. Allerdings benötigt unser „fleißiger Taschencomputer“ dafür fast 20 Minuten. Als relative Häufigkeit erhält man für k = 100 und den Wert 0,73.
Interaktiv ist es möglich, k und n zu verändern, wie die folgende Abbildung zeigt.
-
Interaktive Simulation des Geburtstagsproblems
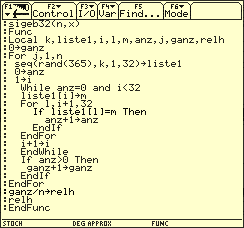
Lösungsvariante 3 (Theoretischer Ansatz)
Für die theoretische Lösung ist es hilfreich, das Gegenereignis zu betrachten, wobei gilt:
bedeutet, dass von den n Personen nicht zwei oder mehr Personen an demselben Tag Geburtstag haben. Der dazugehörige Pfad des Baumdiagramms ist im Testbild (s. unten) angegeben.
Dabei gibt es
- für eine erste Person 365 mögliche Geburtstage,
- für eine zweite Person nur noch 364 Tage, um an einem anderen Tag Geburtstag zu haben als die erste Person,
- und für eine n-te Person nur noch 365 – n +1 verschiedene Tage.
Mithilfe der Multiplikationsregel erhält man:
![]()
Die folgende Tabelle zeigt einige ausgewählte gerundete Werte von :
| n | 2 | 5 | 10 | 15 | 20 | 21 | 22 | 23 |
| 0,003 | 0,027 | 0,117 | 0,253 | 0,411 | 0,444 | 0,476 | 0,507 | |
| n | 24 | 25 | 30 | 32 | 40 | 50 | 60 | 100 |
| 0,538 | 0,569 | 0,706 | 0,753 | 0,891 | 0,970 | 0,994 | 0,999 |
Wertet man diese Tabelle aus, so lässt sich Folgendes feststellen:
- Erstaunlicherweise ist die Wahrscheinlichkeit dafür, dass unter 23 Personen zwei den gleichen Geburtstag haben, bereits größer als 0,5 und damit auch größer als die Wahrscheinlichkeit, dass alle 23 Geburtstage voneinander verschieden sind.
- liegt bereits über 0,99.
- Es ist , d.h., der mit Lösungsvariante 2 gewonnene Wert 0,73 stellt eine gute Näherung dar. Er bestätigt auch die eingangs von Sarahs Onkel geäußerte Vermutung.
Sarah schaut verwundert auf das Ergebnis. „Ich sehe das Ergebnis, allein mir fehlt der Glaube“, lautet ihr Kommentar.
„Ich denke, das liegt daran, dass es dir eigentlich um eine andere Fragestellung geht, nämlich um die Wahrscheinlichkeit, dass mit dir mindestens eine von den 31 anderen Verwandten Geburtstag hat“, entgegnet ihr Onkel.
- Es sei das Ereignis, dass mindestens eine von n Personen an einem bestimmten Tag ebenfalls Geburtstag hat.
Dann ist:
Es ist also tatsächlich unwahrscheinlich, dass unter 31 Personen mindestens eine Person an einem bestimmten Tag (z.B. an dem Tag, an dem Sarah geboren wurde) Geburtstag hat. Dies erklärt auch das Missverständnis von Sarah.
Für das Geburtstagsproblem gibt es verschiedene Verallgemeinerungen:
- Man kann z.B. nach der Wahrscheinlichkeit fragen, dass mindestens drei, vier oder k von n Personen gemeinsam Geburtstag haben.
Eine Antwort würde den hier gegebenen Rahmen sprengen. - Das zugrunde liegende LAPLACE-Experiment braucht nicht genau 365 Ergebnisse zu haben, d.h., die Ergebnismenge kann die Gestalt mit besitzen.
Dann gilt:
Im Alltag tritt das Geburtstagsproblem mitunter in eingekleideter Form auf. Es verbirgt sich beispielsweise nicht selten hinter der Frage nach der Wahrscheinlichkeit dafür, dass ein an sich seltenes Ereignis gleich zweimal an einem Tag (oder relativ kurz hintereinander) auftritt.

