Drei-Sigma-Regel

• Satz: Die Wahrscheinlichkeit, dass eine endliche Zufallsgröße X mit dem Erwartungswert $EX=\mu$ und der Streuung $D^{2}X={\sigma }^2$
  – Werte im $2\sigma \text{-}Intervall\left]\mu -2\sigma ;\mu +2\sigma \right[$ annimmt, beträgt mindestens 0,75;
  – Werte im $3\sigma \text{-}Intervall\left]\mu -3\sigma ;\mu +3\sigma \right[$ annimmt, mindestens $\mathrm{0,}\overline{8}$.

Wir betrachten ein Beispiel.

• Beispiel: Mit welcher Wahrscheinlichkeit weicht die Zufallsgröße X um mehr als 2DX von EX ab?

In einer ersten Stufe der Bearbeitung des Beispiels setzen wir nur die Kenntnis von EX und $D^{2}X$ voraus. Der Vorteil der $\sigma \text{-}\mathrm{Re}gel$ besteht darin, dass sie auch dann angewendet werden kann, wenn man die Wahrscheinlichkeitsverteilung der Zufallsgröße X nicht kennt, sondern nur ihren Erwartungswert EX und ihre Streuung $D^{2}X$.

Es sei $EX=\mathrm{0,125}$ und $D^{2}X=\mathrm{1,609375}$. Nach der $3\sigma \text{-}\mathrm{Re}gel$ erhält man:
$P\left(\left|X-EX\right|\ge 2DX\right)\le \mathrm{0,25}$

Das heißt: Mit einer Wahrscheinlichkeit von höchstens 0,25 weicht die Zufallsgröße X um mehr als 2DX von EX ab.

In einer zweiten Stufe setzen wir zusätzlich die Kenntnis der Wahrscheinlichkeitsverteilung der Zufallsgröße X voraus. Es sei $X\stackrel{\wedge}{=}\left(\begin{array}{ccc}-2& 0& 3\\ \mathrm{0,125}& \mathrm{0,750}& \mathrm{0,125}\end{array}\right).$

Wie man sich überzeugen kann, hat X die oben angegebenen Werte für den Erwartungswert und die Streuung. Jetzt ist es möglich, die gesuchte Wahrscheinlichkeit direkt zu berechnen:
$\begin{array}{l}P\left(\left|X-EX\right|\ge 2DX\right)=P\left(\left|X-\mathrm{0,125}\right|\ge 2\sqrt{\mathrm{1,609375}}\right)\\ =1-P\left(\left|X-\mathrm{0,125}\right|<2\sqrt{\mathrm{1,609375}}\right)\\ =1-P\left(-2\sqrt{\mathrm{1,609375}}+\mathrm{0,125}<X<2\sqrt{\mathrm{1,609375}}+\mathrm{0,125}\right)\\ =1-P\left(X=-2\right)-P\left(X=0\right)\\ =1-\mathrm{0,125}-\mathrm{0,750}=\mathrm{0,125}\end{array}$

Die Zufallsgröße X weicht also mit einer Wahrscheinlichkeit von 0,125 um mehr als 2DX von EX ab.

Das Beispiel zeigt, dass die auf der $3\sigma \text{-}\mathrm{Re}gel$ beruhenden Abschätzungen relativ grob sind. Dies schränkt die Möglichkeiten einer praktischen Nutzung der Regel ein. Trotzdem ist sie nicht ohne praktische Relevanz.

Wir betrachten im Folgenden ein Anwendungsbeispiel.

• Beispiel: Lars Spielmann besitzt noch einen alten, abgenutzten und lädierten Würfel, dessen Beschriftung mit den Zahlen 1 bis 6 teilweise nur noch schwer zu erkennen ist. Trotzdem hängt er an diesem Würfel. Er möchte deshalb gern wissen, ob er ihn noch benutzen kann, wenn das betreffende Würfeln fair ablaufen soll.

Dazu würfelt er 1000-mal mit diesem Würfel und registriert die absoluten Häufigkeiten für die einzelnen Zahlen. Als relative Häufigkeiten erhält er dann die in der folgenden Tabelle enthaltenen Werte

Da Lars Spielmann fair würfeln möchte, muss er von der Annahme ausgehen, dass alle Zahlen gleichwahrscheinlich auftreten, und zwar mit dem Erwartungswert
$\mu =E\left(h_{1000}\left(\left\{2\right\}\right)\right)=P\left(\left\{2\right\}\right)=\mathrm{0,1}\overline{6}$

und der Standardabweichung
$\sigma =\sqrt{D^2\left(h_{1000}\left(\left\{2\right\}\right)\right)}=\sqrt{\frac{1}{1000}\cdot \left(\frac{1}{6}-\frac{1}{36}\right)}\approx \mathrm{0,0118.}$

Das zugehörige $3\sigma \text{-}Intervall$ist $\left]\mu -3\sigma ;\mu +3\sigma \right[=\left]\mathrm{0,131...};\mathrm{0,202...}\right[$.

Da die relativen Häufigkeiten für die Würfelzahlen 2 und 5 außerhalb des $3\sigma \text{-}Intervalls$ liegen, wird sich Lars Spielmann wohl von diesem Würfel trennen müssen, denn die angenommene Gleichwahrscheinlichkeit der Augenzahlen kann mit einer Fehlerwahrscheinlichkeit von höchstens $\mathrm{0,}\overline{1}$ verworfen werden.

Eigene Würfelergebnisse kann man mit dem „gezinkten Taschenrechnerwürfel “ interaktiv gewinnen.

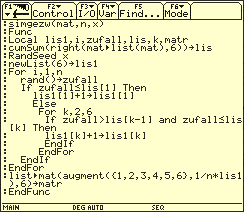
So ist es z.B. möglich, zu untersuchen,

1. wie stark man den Würfel „zinken“ muss, um bei festen n relative Häufigkeiten zu bekommen, die außerhalb des $3\sigma \text{-}Intervall$ liegen, oder
2. wie oft man einen speziell „gezinkten“ Würfel werfen muss, um relative Häufigkeiten zu erhalten, die außerhalb des $3\sigma \text{-}Intervall$ liegen.

Zur Demonstration wird die „Zinkung“
$\left(\begin{array}{cccccc}1& 2& 3& 4& 5& 6\\ \mathrm{0,15}& \mathrm{0,31}& \mathrm{0,17}& \mathrm{0,16}& \mathrm{0,07}& \mathrm{0,14}\end{array}\right)$
gewählt.

Mithilfe des Programms simgezw(mat,n,x) erhält man z.B. die folgenden Simulationsergebnisse:

Vergleicht man die relativen Häufigkeiten mit dem jeweiligen $3\sigma \text{-}Intervall$, so sieht man, dass bei dieser Simulation die relativen Häufigkeiten erstmals für n = 100 außerhalb des $3\sigma \text{-}Intervalls$ liegen.

Bei einer $N\left(0;1\right)\text{-verteilten}$ Zufallsgröße X mit $\mu =0$ und $\sigma =1$ verschärft sich die Aussage der $3\sigma \text{-}\mathrm{Re}gel$ zu
$P\left(X\in \left[-3;3\right]\right)={\displaystyle \underset{-3}{\overset{3}{\int }}\varphi \left(x\right)dx>\mathrm{0,99}}$
(wobei $\varphi$ die Dichtefunktion von X ist).

Unter Beachtung der Symmetrie der Glockenkurve gilt:
${\displaystyle \underset{-\infty }{\overset{-3}{\int }}\varphi \left(x\right)dx<\frac{1}{2}\cdot \left(1-\mathrm{0,99}\right)}=\mathrm{0,005.}$

Somit begeht man beim Berechnen von
$\Phi \left(a\right)={\displaystyle \underset{-\infty }{\overset{a}{\int }}\varphi \left(x\right)dx}$
auf zwei Dezimalen gerundet keinen Fehler, wenn dabei die untere Integrationsgrenze $-\infty$ durch $-3$ ersetzt wird, was einen beträchtlichen Zeitgewinn bei der Nutzung des TI-92 bedeutet.