Hyperbolische Funktionen (Hyperbelfunktionen)

Unter Verwendung der Exponentialfunktion $y=e^x$ lassen sich weitere Funktionen, die sogenannten hyperbolischen Funktionen (bzw. Hyperbelfunktionen), definieren:

• Sinus hyperbolicus (bzw. Hyperbelsinus)
  $\sinh x:=\frac{1}{2}\left(e^x-e^{-x}\right)(x\in ℝ)$
• Cosinus hyperbolicus (bzw. Hyperbelkosinus)
  $\cosh x:=\frac{1}{2}\left(e^x+e^{-x}\right)(x\in ℝ)$

Anmerkung: Wie aus dem Funktionsverlauf zu erkennen ist, hat der Graph der Funktion $y=\cosh x$ die Form einer Kette, wenn man diese an ihren Enden aufhängt. Deshalb wird diese Kurve auch als Kettenlinie bezeichnet.

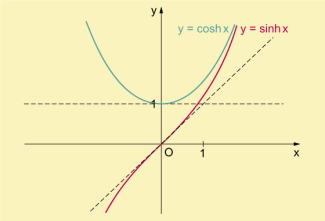
Entsprechend der Beziehungen bei den trigonometrischen Funktionen kann man noch ergänzen:

• Tangens hyperbolicus (bzw. Hyperbeltangens)
  $\tanh x:=\frac{\sinh x}{\cosh x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}(x\in ℝ)$
• Cotangens hyperbolicus (bzw. Hyperbelkotangens)
  $\coth x:=\frac{\cosh x}{\sinh x}=\frac{e^x+e^{-x}}{e^x-e^{-x}};(x\in ℝ;x\ne 0)$

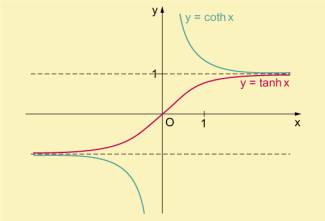
Die wichtigsten Eigenschaften der hyperbolischen Funktionen sind in der folgenden Übersicht zusammengefasst.

Auf einige dieser Eigenschaften wird im Folgenden näher eingegangen.

Symmetrieverhalten

Es gilt:
$\begin{array}{l}\sinh (-x)=\frac{1}{2}\left(e^{-x}-e^x\right)=-\frac{1}{2}\left(e^x-e^{-x}\right)=-\sinh x\\ \cosh (-x)=\frac{1}{2}\left(e^{-x}+e^x\right)=\frac{1}{2}\left(e^x+e^{-x}\right)=\cosh x\end{array}$
Die Funktion $y=\sinh x$ ist demzufolge eine ungerade Funktion und ihr Graph liegt zentralsymmetrisch (punktsymmetrisch) zum Koordinatenursprung O; die Funktion $y=\cosh x$ ist gerade mit der y-Achse als Symmetrieachse.

Verhalten im Unendlichen

Mithilfe der Grenzwertsätze erhält man:
$\begin{array}{l}\underset{x\to \infty }{\lim }\sinh x=\frac{1}{2}\left(\underset{x\to \infty }{\lim }{e}^x-\underset{x\to \infty }{\lim }\frac{1}{e^x}\right)=\infty \\ \underset{x\to \infty }{\lim }\cosh x=\frac{1}{2}\left(\underset{x\to \infty }{\lim }{e}^x+\underset{x\to \infty }{\lim }\frac{1}{e^x}\right)=\infty \end{array}$
Weiter ist:
$\underset{x\to -\infty }{\lim }\sinh x=\underset{t\to \infty }{\lim }\sinh (-t)=-\underset{t\to \infty }{\lim }\sinh t=-\infty$
Wegen der Symmetrie zur x-Achse ist auch $\underset{x\to -\infty }{\lim }\cosh x=\infty$.

Monotonieverhalten

Aus $x_1<x_2$ folgt wegen der Monotonie der Exponentialfunktion über ihrem gesamten Definitionsbereich $e^{x_1}<e^{x_2}$ und damit $e^{x_1}-e^{x_2}<0$.
Für den Sinus hyperbolicus gilt somit
$\begin{array}{c}\sinh x_1-\sinh x_2=\frac{1}{2}\left[\left(e^{x_1}-e^{-x_1}\right)-\left(e^{x_2}-e^{-x_2}\right)\right]\\ =\frac{1}{2}\left[\left(e^{x_1}-e^{x_2}\right)+\left(e^{-x_2}-e^{-x_1}\right)\right]\\ =\frac{1}{2}\left[\left(e^{x_1}-e^{x_2}\right)+\left(e^{x_1-(x_1+x_2)}-e^{x_2-(x_1+x_2)}\right)\right]\\ =\frac{1}{2}\left[\left(e^{x_1}-e^{x_2}\right)+e^{-(x_1+x_2)}\left(e^{x_1}-e^{x_2}\right)\right]\\ =\frac{1}{2}\left(e^{x_1}-e^{x_2}\right)\left(1+e^{-(x_1+x_2)}\right)<\mathrm{0,}\end{array}$
denn $e^{x_1}-e^{x_2}<0$ und $1+e^{-(x_1+x_2)}>0$.
Die Funktion $y=\sinh x$ ist über dem gesamten Definitionsbereich monoton wachsend (steigend).
Für die Funktion $y=\cosh x$ ist bei der Untersuchung des Monotonieverhaltens eine Fallunterscheidung für positive und negative x-Werte vorzunehmen. Durch analoge Umformungen wie beim Sinus hyperbolicus lässt sich zeigen, dass die Funktion für $x\in \left]-\infty ;0\right[$ monoton fallend und für $x\in \left]0;+\infty \right[$ monoton wachsend ist.

Extremwerte

Zur Untersuchung der hyperbolischen Funktionen auf Extrema werden deren Ableitungen benötigt. Es gilt:
$\begin{array}{l}y\text{'}=(\sinh x)\text{'}={\left[\frac{1}{2}\left(e^x-e^{-x}\right)\right]}^{\text{'}}=\frac{1}{2}\left(e^x+e^{-x}\right)=\cosh x\\ y\text{'}=(\cosh x)\text{'}={\left[\frac{1}{2}\left(e^x+e^{-x}\right)\right]}^{\text{'}}=\frac{1}{2}\left(e^x-e^{-x}\right)=\sinh x\end{array}$
Da $\cosh x\ne 0$ für alle $x\in R$ gilt, besitzt die Funktion $y=\sinh x$ keine Extremwerte. Dagegen hat Funktion $y=\cosh x$ an der Stelle x = 0 ein Minimum, also ist der Punkt P(0; 1) Minimumpunkt.

Funktionsverlauf

Die Graphen von $y=\sinh x$und $y=\cosh x$ haben keine Ähnlichkeit mit den Graphen der trigonometrischen Funktionen.

Analogien zu den trigonometrischen Funktionen ergeben sich in den Additionstheoremen und weiteren (wie aus der Trigonometrie bekannten) Beziehungen. So gilt:

$\begin{array}{l}\sinh (x\pm y)=\sinh x\cosh y\pm \cosh x\sinh x\\ \cosh (x\pm y)=\cosh x\cosh y\pm \sinh x\sinh x\end{array}$
Weiter ist:
$\begin{array}{l}\sinh x\pm \sinh y=2\sinh \frac{x\pm y}{2}\cosh \frac{x\mp y}{2}\\ \cosh x+\cosh y=2\cosh \frac{x+y}{2}\cosh \frac{x-y}{2}\\ \cosh x-\cosh y=2\sinh \frac{x+y}{2}\sinh \frac{x-y}{2}\end{array}$

Statt des sogenannten „trigonometrischen Pythagoras“ gilt (wie man durch Einsetzen überprüfen kann) die folgende Beziehung:
${\cosh }^{2}x-{\sinh }^{2}x=1$

Diese Formel lässt erkennen, dass $\cosh x$ und $\sinh x$ der Gleichung einer gleichseitigen Hyperbel der Form $x^2-y^2=a^2$ genügen. Daraus resultiert die Bezeichnung hyperbolische Funktionen bzw. Hyperbelfunktionen.

Die hyperbolischen Funktionen traten in ihren Grundlagen implizit u.a. bereits bei ISAAC NEWTON (1623 bis 1727) und ABRAHAM DE MOIVRE (1667 bis 1754) auf.
Die Theorie dieser Funktionen begründete der italienische Mathematiker VINCENZO RICCATI (1707 bis 1775) unter Verwendung geometrischer Betrachtungen. Im Jahre 1768 kam dann JOHANN HEINRICH LAMBERT (1728 bis 1777) auf die Idee, die hyperbolischen Funktionen für die Trigonometrie zu nutzen.