Permutationen
- Beispiel: Anna, Beate und Stefan, die Schülervertreter des Shakespeare-Gymnasiums, sind mit einem wichtigen Anliegen auf dem Weg zu ihrem Schulleiter. Sie haben Glück, die Zimmertür des Schulleiters steht etwas offen, sodass sie ihre Köpfe hindurchstecken können.
„Wollt ihr was?“,
werden sie leicht mürrisch, aber nicht unhöflich angesprochen. „Ja“, entgegnet Beate mit fester Stimme, „im Namen der Schüler unseres Gymnasiums möchten wir eine Verkürzung der Unterrichtsstunden um fünf Minuten zugunsten der Pausen fordern!“
Zuerst herrscht einen Moment lang Stille, dann kommt die ungläubige Rückfrage des Schulleiters:
„ Was wollt ihr?“
Die Schülervertreter hat der Mut verlassen. Sie schweigen. Im gleichen Maße wächst beim Schulleiter die Erregung und seine Worte bekommen einen leicht drohenden Unterton:
„ Ihr wollt was?“
Die Schülervertreter sind verunsichert. Der Schulleiter sucht nach einem Ausweg. Da fällt ihm der Namenspatron des Gymnasiums ein und mit den Worten
„Was ihr wollt!“
drängt er die Schüler mit einem Anflug von Lachen aus dem Zimmer.
Die Schüler gehen verdattert von dannen, nicht wissend was sie davon halten sollen.
Anna stellt lakonisch fest: „Zwei Permutationen hat er vergessen!“
„Was, bitte wie?“, fragt Stefan nun vollends verwirrt ...
Das Wort Permutation geht auf das lateinische permutare zurück, was mit verändern, wechseln oder vertauschen übersetzt werden kann.
- Definition: Jede mögliche Anordnung von n Elementen als n-Tupel, in der alle Elemente verwandt werden, heißt Permutation dieser n Elemente.
bezeichnet die Anzahl der Permutationen bei n Elementen.
Im obigen Beispiel wurden vom Schulleiter die Worte was, ihr und wollt auf vier verschiedenen Weisen angeordnet, d.h. er hat vier Permutationen benutzt.
Einen Überblick über die Anzahl aller möglichen Permutationen kann man sich verschaffen, indem man sich bewusst macht, dass es drei Möglichkeiten gibt, die erste Stelle des Drei-Wort-Satzes zu besetzen. Wenn die erste Stelle besetzt ist, gibt es nur noch zwei Möglichkeiten, die zweite Stelle zu belegen. Sind die erste und die zweite Stelle entschieden, gibt es für die dritte Stelle nur noch eine Möglichkeit, d.h., die Anzahl der Möglichkeiten ist . Anna hat also Recht mit ihrer Bemerkung, dass zwei Permutationen vom Schulleiter nicht verwandt wurden.
Diagramm zur Veranschaulichung von Permutationen
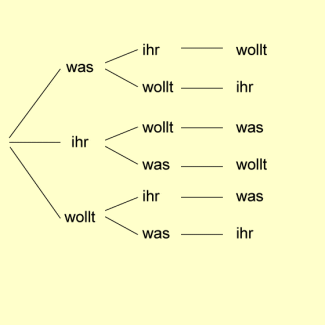
Das Berechnen aller möglichen Permutationen von n Elementen ist eine typische Aufgabenstellung der Kombinatorik. Schon in der im 13. Jahrhundert erschienenen Schrift „De Vetula“ wurde bei der mathematischen Beantwortung der Frage, mit welchen Erfolgsaussichten auf Augenzahlen zwischen 3 und 18 beim Wurf mit drei Würfeln gesetzt werden kann, mit Permutationen gearbeitet.
Von n verschiedenen Elementen gibt es Möglichkeiten der Anordnung. Da es sich um verschiedene Elemente handelt, spricht man auch von Permutationen ohne Wiederholung . Für die Anzahl derartiger Permutationen gilt also:
Für definiert man zweckmäßigerweise . Da eine
n-elementige Menge nur verschiedene Objekte enthält, gibt es Möglichkeiten, ihre Elemente anzuordnen.
Sind unter den anzuordnenden Objekten Elemente gleich, so reduziert sich die Anzahl der möglichen Permutationen.
Für die Anzahl der Permutationen von n Elementen mit Wiederholung (n Elemente, von denen je untereinander gleich sind) gilt:
Ein schrittweises Berechnen der Werte von zeigt, dass die Zahlen für wachsendes n schnell sehr groß werden. Für große n kann man aber Näherungsformeln verwenden, z.B. die folgenden:
Mithilfe computergestützter Simulationen kann man sich von der Güte der Näherungsformeln für verschiedene n überzeugen.
Überprüfung der Güte von Näherungsformeln zur Berechnung der Permutationenanzahl
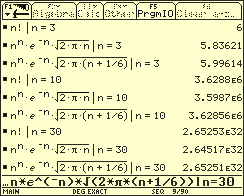
Das Bestimmen der Anzahl von Permutationen wird in der Stochastik vor allem beim Berechnen von LAPLACE-Wahrscheinlichkeiten benötigt.
Permutationen können auch als Funktionen interpretiert werden. In diesem Sinne nennt man eine eineindeutige Abbildung einer endlichen Menge auf sich eine Permutation dieser Menge. Um etwa die Permutation der Menge darzustellen, verwendet man die folgende Schreibweise:
Dieser Ansatz ermöglicht es, Eigenschaften und Strukturen von Permutationen aufzudecken und Verkettungen zwischen ihnen zu vollziehen. Um die durch Permutationen vermittelten Abbildungen anschaulich verfolgen zu können, benutzt man verschiedene Diagramme (siehe folgende Abbildung).
Diagramme zur Veranschaulichung von Permutationen
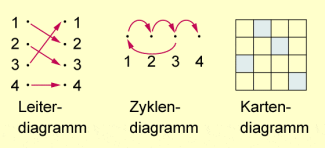
In der Rangkorrelationsanalyse, einem speziellen Teil der Korrelationsanalyse, untersucht man, inwieweit eine bestimmte Permutation zufälligen Charakter besitzt.
- Beispiel: Ein Autohersteller hat von einem Subunternehmen zwei verschiedene Sendungen des gleichen Bauteils erhalten. Er möchte nun wissen, ob man die Hypothese annehmen sollte, dass die erste Lieferung hinsichtlich eines bestimmten Parameters wesentlich kleinere Messwerte aufweist als die zweite.
Dazu werden der ersten Lieferung n und der zweiten m Bauteile „auf gut Glück“ entnommen und jeweils der interessierende Parameter gemessen. In der Reihenfolge der durchgeführten Messungen erhält man die Werte .
Ordnet man die Messwerte der Größe nach, ergibt sich eine bestimmte Permutation, z.B. . Wenn dies eine „Zufallspermutation“ ist, so wäre dies ein Indiz dafür, dass sich die beiden Lieferungen hinsichtlich des untersuchten Parameters nicht wesentlich voneinander unterscheiden.
Als Maß für die Zufälligkeit einer Permutation kann man z.B. die Anzahl der sogenannten Inversionen benutzen, wobei zwei Elemente einer Permutation eine Inversion bilden, wenn ihre Anordnung im Vergleich zu „natürlichen“ umgekehrt ist, wenn also bei obiger Hypothese ein nach einem steht.
Anordnung Berechnung ohne Wiederholung Funktion Elemente Mathcad interaktives Rechenbeispiel Rangkorrelationsanalyse mit Wiederholung Inversion
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 