Pseudozufallszahlen

Um möglichst gerecht und objektiv vorzugehen, nutzt Lehrer Stochasius die Randomfuktion seines Taschencomputers, um einen Schüler für eine mündliche Leistungskontrolle zu bestimmen. Trotzdem haben einige Schüler Zweifel an diesem Verfahren (vor allem dann, wenn ein Schüler zweimal hintereinander „ausgewürfelt“ wurde). Der Klassenprimus stellt überhaupt infrage, dass ein solch streng deterministisch arbeitendes Gerät wie ein Rechner Zufallsziffern erzeugen könne.

Vor diesem Problem standen die Entwickler von Computern ursprünglich auch. Man versuchte anfangs, Zufallsziffern mithilfe realer Vorgänge mit zufälligem Ergebnis (z.B. radioaktiver Zerfall), die in einen Computer eingebaut wurden, zu erzeugen. Dem war aber kein großer Erfolg beschieden, zumal man herausfand, dass es auch mit deterministischen (rekursiven) Algorithmen möglich ist, Ziffernfolgen, sogenannte Pseudozufallszahlen, zu erstellen, die weitgehend dieselben Eigenschaften wie echte Zufallszahlen besitzen.

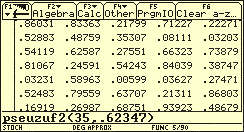
Im Folgenden wird ein Algorithmus zum Erzeugen fünfstelliger Pseudozufallszahlen angegeben:

1. $x_0$ Startzahl zwischen 0 und 1 mit fünf Stellen nach dem Komma, z.B. 0,62347
2. $x_1=173\cdot x_0-\mathrm{int}\left(173\cdot x_0\right)=\mathrm{0,86031}$
3. ...
4. $x_n=173\cdot x_{n-1}-\mathrm{int}\left(173\cdot x_{n-1}\right)$

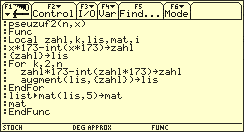
Dieser Algorithmus – es gibt auch andere – ist ein periodischer Pseudozufallsgenerator, d.h. nach einer gewissen Anzahl von Schritten wiederholen sich die Startzahl (es gibt nur ${10}^5-1$ verschiedene infrage kommende Zufallszahlen aus $\left]0;1\right[$ mit fünf Dezimalstellen, also kehrt die Startzahl $x_0$ spätestens als $x_{{10}^5-1}$ wieder) und damit auch die folgenden Zahlen.

Es sollte deshalb das Bestreben sein, die in den Algorithmus eingehenden Konstanten so zu wählen, dass es möglichst lange dauert, bis sich die Startzahl wiederholt und dass die Zufallszahlen gewissen Gütekriterien genügen. Als günstig hat sich in diesem Sinne der Faktor 173 erwiesen. Positiv wirken sich als Faktoren auch die Zahlen 117, 123, 133, 147, 163, 187 oder 197 aus. Die Startzahl sollte als letzte Ziffer eine 1, 3, 7 oder 9 haben. Fatale Auswirkungen hätte die 0,5, was man auch interaktiv überprüfen könnte.

Nicht weniger wichtig als das Gewinnen von Zufallszahlen ist die Überprüfung ihrer Güte, denn aus der Analyse einer zufälligen Stichprobe werden oftmals weitreichende Entscheidungen getroffen, sei es in Politik, Wirtschaft oder Gesellschaft. So entscheidet z.B. die durch eine zufällige Stichprobe gewonnene Einschaltquote über das Wohl und Wehe von Fernsehsendungen.
Zu den häufig angewandten Gütekriterien zählen die folgenden:

1. Für die relativen Häufigkeiten des Auftretens der zehn Ziffern müsste gelten:
   $h_n\left(\left\{0\right\}\right)\approx h_n\left(\left\{1\right\}\right)\approx \mathrm{...}\approx h_n\left(\left\{9\right\}\right)\approx \mathrm{0,1}$
2. Für die relativen Häufigkeiten des Auftretens der Ziffernpaare müsste gelten:
   $h_n\left(\left\{\left(0;0\right)\right\}\right)\approx h_n\left(\left\{\left(1;1\right)\right\}\right)\approx \mathrm{...}\approx h_n\left(\left\{\left(9;9\right)\right\}\right)\approx \mathrm{0,01}$
3. Die ${10}^3$ Zifferntripel, die ${10}^4$ Ziffernquadrupel, ... besitzen die analogen Eigenschaften wie die in (1) und (2) genannten.
4. Beim Maximumtest, für den die Zufallszahl als Folge von Zifferntripel dargestellt worden ist, müsste gelten:
   $\begin{array}{l}{h}_n\left(\left\{\text{die}\text{mittlere}\text{Ziffer}\text{ist}\text{größer}\text{als}\text{ihre}\text{Nachbarn}\right\}\right)\\ \approx \frac{1^2+2^2+\mathrm{...}+9^2}{1000}=\mathrm{0,285}\end{array}$
5. Beim Pokertest, für den die Zufallszahl als Folge von 5-Tupeln dargestellt worden ist, müssten die nachfolgenden Näherungen für die Ziffern des 5-Tupels gelten:
   $\begin{array}{l}{h}_n\left(\left\{alle\text{Ziffern}\text{des}\text{5-Tupels}\sin dverschieden\right\}\right)\\ \approx \frac{10\cdot 9\cdot 8\cdot 7\cdot 6}{{10}^5}=\mathrm{0,3024}\end{array}$
   $\begin{array}{l}{h}_n\left(\left\{\text{genau}\text{vier}\text{verschiedene}\text{Ziffern}\text{im}\text{5-Tupel}\right\}\right)\\ =h_n\left(\left\{\text{genau}\text{eine}\text{Ziffer}\text{tritt}\text{genau}\text{zweimal}\text{auf}\right\}\right)\\ \approx \left(\begin{array}{c}5\\ 2\end{array}\right)\cdot \frac{10\cdot 1\cdot 9\cdot 8\cdot 7}{{10}^5}=\mathrm{0,5040}\end{array}$
   $\begin{array}{l}{h}_n\left(\left\{\text{genau}drei\text{verschiedene}\text{Ziffern}\text{und}\text{davon}genauzweidoppelt\right\}\right)\\ \approx \left(\begin{array}{c}5\\ 2\end{array}\right)\cdot \left(\begin{array}{c}3\\ 2\end{array}\right)\frac{10\cdot 1\cdot 9\cdot 1\cdot 8}{{10}^5}=\mathrm{0,2160}\\ usw.\end{array}$
6. Beim Run-Test stimmen die relativen Häufigkeiten für das Auftreten langer Sequenzen von geraden Ziffern, von Primzahlen o.Ä. mit den entsprechenden zu berechnenden Wahrscheinlichkeiten gut überein.

Um die Güte einer Zufallszahl zu bestimmen, genügt es nicht, nur einen der obigen Tests (oder einen ähnlichen Test) durchzuführen.
Die Zufallszahl $\mathrm{0123456890123456789012...}$ beispielsweise genügt zwar hervorragend (1), ist aber nach (2) als eine sehr schlechte Zufallszahl einzustufen.