Winkelfunktionen y = f(x) = a sin (bx + c)

Besonders bei der mathematischen Beschreibung von Schwingungsvorgängen wird häufig von Winkelfunktionen, speziell der Sinusfunktion mit Gleichungen der Form $y = f (x) = a \cdot \sin (b x + c)$ Gebrauch gemacht.
Bezogen auf den Graphen von f nennt man deshalb a auch die Amplitude der Sinuskurve, b deren Frequenz und c ihre Phasenverschiebung.

Ausgehend von der Funktion $y = f (x) = \sin x$ und ihrem Graphen sollen zunächst die Eigenschaften von Funktionen mit der Gleichung $y = f (x) = a \cdot \sin (b x + c)$ für verschiedene Werte der darin auftretenden Parameter untersucht werden.

(1) Mit b = 1, c = 0 und $a \neq 0$ erhält man aus $y = f (x) = a \cdot \sin (b x + c)$ die Gleichung y = $f_{1}$ (x) = a sin x.
Für a = – 1, a = 0,5, a = 1 und a = 3 sind die Graphen der Funktionen in der folgenden Abbildung dargestellt.

Graphen der Funktionen mit y = a sin x

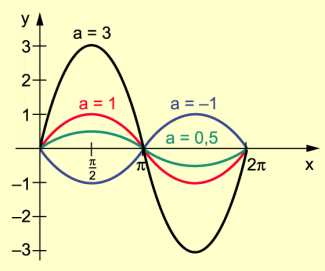
Folgende Eigenschaften der Funktionen sind erkennbar:

Die Funktionen sind periodisch mit der gemeinsamen Periode $2 π$ .
Da der Maximum- bzw. der Minimumpunkt von $y = f (x) = \sin x$ die Ordinate 1 bzw. – 1 hat, besitzt die Ordinate dieser Punkte für die Funktionen $f_{1}$ (x) = a sin x den Werte a bzw. – a.
Falls a > 1, geht der Graph von $f_{1}$ durch Streckung in Richtung der y-Achse aus dem Graphen von f hervor.
Falls 0 < a < 1, geht der Graph von $f_{1}$ durch Stauchung in Richtung der y-Achse aus dem Graphen von f hervor.
Falls a < 0, geht der Graph von $f_{1}$ durch Spiegelung an der x-Achse und anschließender Streckung oder Stauchung in Richtung der y-Achse aus dem Graphen von f hervor.
Die Funktionen y = $f_{1}$ (x) = a sin x haben die gemeinsamen Nullstellen $x = k \cdot π (k \in ℤ)$ .

In der Funktion f mit y = f(x) = a · sin x heißt a $(a \neq 0)$ die Amplitude der Sinuskurve; a gibt den maximalen, – a den minimalen Ordinatenwert an.

(2) Mit a = 1, c = 0 und $b \neq 0$ erhält man aus $y = f (x) = a \cdot \sin (b x + c)$ die Gleichung y = $f_{2}$ (x) = sin bx.
Für b = – 1, b = 0,5, b = 1 und b = 2 sind die Graphen der Funktionen in der folgenden Abbildung dargestellt.

Graphen der Funktionen mit y = sin bx

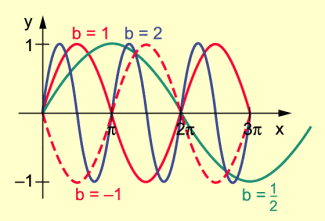
Folgende Eigenschaften der Funktionen sind erkennbar:

Da die Funktion $y = f (x) = \sin x$ an den Stellen $k \cdot π (k \in ℤ)$ Nullstellen besitzt, dort also den Wert 0 annimmt, trifft dies für die Funktion $f_{2}$ (x) = sin bx dann zu, wenn $b \cdot x = k \cdot π, also x = \frac{π}{b} \cdot k (k \in ℤ)$ .
Die Funktionen y = $f_{2}$ (x) = sin bx sind periodisch, besitzen jedoch die von b abhängige unterschiedliche Periodenlänge $\frac{2 π}{| b |}$ .
Da der Maximum- bzw. der Minimumpunkt von y = sin x die Ordinate 1 bzw. – 1 hat, gilt dies auch für alle Graphen von
y = $f_{2}$ (x) = sin bx.
Falls b > 1, geht der Graph von $f_{2}$ durch Stauchung in Richtung der x-Achse aus dem Graphen von f hervor.
Falls 0 < b < 1, geht der Graph von $f_{2}$ durch Streckung in Richtung der x-Achse aus dem Graphen von f hervor.
Falls b < 0, geht der Graph von $f_{2}$ wegen $\sin (- x) = - \sin x$ durch Spiegelung an der x-Achse und anschließender Streckung oder Stauchung in Richtung der x-Achse aus dem Graphen von f hervor.

In der Funktion f mit y = f(x) = sin bx heißt b $(b \neq 0)$ die Frequenz der Sinuskurve. Die Frequenz gibt die Anzahl der vollständigen Perioden in einem Intervall der Länge $2 π$ an.

(3) Mit a = 1, b = 1 und c $\neq$ 0 erhält man aus $y = f (x) = a \cdot \sin (b x + c)$ die Gleichung y = $f_{3}$ (x) = sin(x + c).
Für $c = - \frac{π}{3}, c = 0 und c = \frac{π}{3}$ sind die Graphen der Funktionen in der folgenden Abbildung dargestellt.

Graphen der Funktionen mit y = sin (x + c)

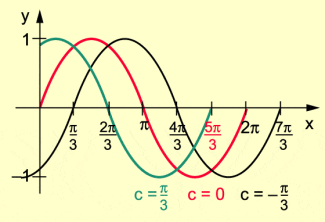
Folgende Eigenschaften der Funktionen sind erkennbar:

Da die Funktion $y = f (x) = \sin x$ an den Stellen $k \cdot π (k \in ℤ)$ Nullstellen besitzt, dort also den Wert 0 annimmt, trifft dies für die Funktion $f_{3}$ (x) = sin(x + c) dann zu , wenn $x + c = k \cdot π, a l s o x = k \cdot π (k \in ℤ) .$
Die Funktionen y = $f_{3}$ (x) = sin(x + c) sind periodisch mit der gemeinsamen Periode $2 π$ .
Da der Maximum- bzw. der Minimumpunkt von $y = f (x) = \sin x$ die Ordinate 1 bzw. – 1 hat, gilt dies auch für alle Graphen von y = $f_{3}$ (x) = sin(x + c).
Falls c > 0, geht der Graph von $f_{3}$ durch Verschiebung nach links in Richtung der x-Achse aus dem Graphen von f hervor.
Falls c = 0, stimmen die Funktionsgleichungen von f und $f_{3}$ und folglich auch ihre Graphen überein.
Falls c < 0, geht der Graph von $f_{3}$ durch Verschiebung nach rechts in Richtung der x-Achse aus dem Graphen von f hervor.

In der Funktion f mit y = f(x) = sin (x + c) heißt c die Phasenverschiebung der Sinuskurve.

Folgende Eigenschaften der Funktionen sind erkennbar bzw. mithilfe von (1) bis (3) berechenbar:

Bild

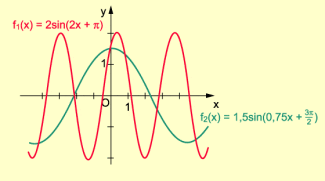
(4) Mit $a \neq 1, b \neq 1 und c \neq 0$ erhalten wir die Funktionen $y = f (x) = a \cdot \sin (b x + c)$ , in denen die in (1) bis (3) beschriebenen Eigenschaften miteinander verknüpft sind.
Für a = 2, b = 2 und $c = \frac{π}{2}$ sowie a = 1,5; b = 0,75 und $c = \frac{3 π}{2}$
sind die Graphen der Funktionen $f_{1}$ bzw. $f_{2}$ sowie $y = f (x) = \sin x$ in der folgenden Abbildung dargestellt.

Graphen der Funktionen mit y = a sin (bx + c)

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel

Angaben zum Lexikon

Impressum

Winkelfunktionen y = f(x) = a sin (bx + c)

Rechtliches

Einloggen