Asymptoten (asymptotische Linien)
Untersucht man ganzrationale Funktionen für beliebige große bzw. kleine x-Werte, so werden auch die Funktionswerte beliebig groß oder klein:
Für gilt .
Völlig verschieden davon ist das Verhalten gebrochenrationaler Funktionen der Form
.
Deren Graphen schmiegen sich für beliebig groß bzw. klein werdende Argumente immer mehr an eine Gerade an. Derartige Geraden werden Asymptoten des Graphen der Funktion genannt. Man unterscheidet zwischen waagerechten (horizontalen) und schiefen Asymptoten sowie asymptotischen Linien bzw. Kurven.
Anmerkung: Gelegentlich werden auch die Polgeraden bei vorhandenen Definitionslücken als senkrechte (vertikale) Asymptoten bezeichnet.
Wie das Verhalten einer gebrochenrationalen Funktion für im Einzelnen aussieht, hängt vom Grad n der Zählerfunktion p(x) und vom Grad m der Nennerfunktion q(x) ab. Dabei lassen sich folgende Fälle unterscheiden:
- Fall:
Sei mit und eine gebrochenrationale Funktion, die für alle definiert ist.
-
Waagerechte Asymptote (x-Achse)
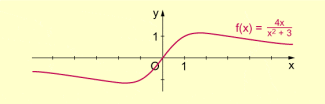
Um Aussagen über das „Grenzverhalten“ der Funktion f machen zu können, sind die Grenzwerte zu bilden. Es gilt:
In dem Fall ist also die x-Achse waagerechte Asymptote.
- Fall:
Gegeben sei die Funktion .
Diese Funktion hat an der Stelle eine Polstelle.
-
Waagerechte Asymptote (Parallele zur x-Achse)
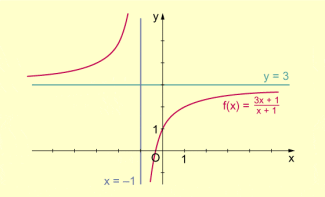
Für die Grenzwerte ergibt sich:
Das heißt, die Gerade ist eine waagerechte Asymptote.
- Fall:
Bei der Funktion ist der Grad der Zählerfunktion um 1 größer als der Grad der Nennerfunktion.
-
Schiefe Asymptote (Winkelhalbierende y = x)
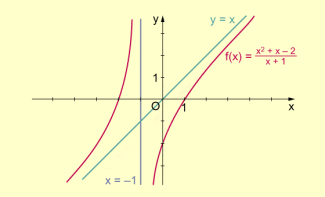
Um eine genaue Aussage über das Verhalten von f(x) für machen zu können, dividiert man das Zählerpolynom durch das Nennerpolynom, dadurch wird der Funktionsterm in eine Summe aus einem ganzrationalen und einem gebrochenrationalen Term zerlegt:
Werden jetzt Betrachtungen zum Grenzwertverhalten der Funktion f durchgeführt, so erkennt man, dass sich die Funktionswerte von f für immer weniger von denen der Funktion unterscheiden, da der Term gegen null strebt.
Das heißt, die Gerade mit der Gleichung ist schiefe Asymptote.
- Fall:
Die Funktion ist für alle definiert.
Durch Polynomdivision erhält man .
-
Asymptotische Linie
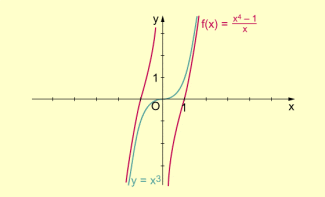
Dann gilt für das Grenzwertverhalten:
Da der Term für gegen null strebt, wird der Unterschied der Funktionswerte von f(x) und denen von immer kleiner. Das bedeutet aber, dass sich der Graph von f asymptotisch an den Graphen von nähert, er wird als asymptotische Kurve des Graphen von f bezeichnet.
Zusammenfassend lässt sich Folgendes feststellen:
Der Graph einer gebrochenrationalen Funktion der Form
hat für im Falle
- die x-Achse als waagerechte Asymptote;
- die Gerade mit der Gleichung als waagerechte Asymptote;
- eine schiefe Asymptote, deren Gleichung man durch Polynomdivision bestimmt.
- eine asymptotische Linie als Näherungskurve, deren Gleichung man ebenfalls durch Polynomdivision bestimmt.

