William George Horner
WILLIAM GEORGE HORNER wurde im Jahre 1786 (das genaue Geburtsdatum ist nicht bekannt) im englischen Bristol geboren. Seine Ausbildung erhielt er an der dortigen Kingswood School. Bereits im Alter von 14 Jahren soll HORNER als Hilfslehrer an dieser Schule gearbeitet haben, um vier Jahre später deren Rektor zu werden. Im Jahre 1809 verließ er Bristol und gründete seine eigene Schule in Bath.
HORNERS (einziger) Beitrag zur Mathematik besteht in der Entwicklung eines Verfahrens zur Berechnung von Werten eines Polynoms (einer ganzrationalen Funktion)
.
Hornersches Verfahren am Beispiel einer ganzrationalen Funktion dritten Grades
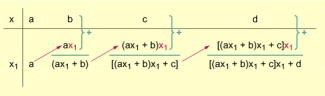
Dieses sogenannte Hornerverfahren (bzw. hornersche Schema) basiert auf einer geschickten Ausklammerung der folgenden Art:
HORNER reichte dieses Verfahren 1819 bei der Royal Society ein, und es wurde einige Jahre später in den Philosophical Transactions of the Royal Society veröffentlicht.
Bereits einige Jahre zuvor hatte der italienische Mathematiker PAOLO RUFFINI (1765 bis 1822) eine ähnliche Methode angegeben und damit eine Goldmedaille in einem Wettbewerb zum Lösen algebraischer Gleichungen gewonnen.
Aber weder HORNER noch RUFFINI sind die eigentlichen Entdecker des dem hornerschen Schema zugrunde liegenden Verfahrens: Bereits 500 Jahre früher ist es in China von CHU SHIH-CHIEH (auch ZHU SHI-JIE, etwa 1270 bis 1330) benutzt worden.
Im 19. sowie in der ersten Hälfte des 20. Jahrhunderts nahm das Verfahren einen bedeutenden Platz in den Lehrbüchern der Algebra ein. Dies ist dadurch begründet, dass der schottische Mathematiker und Logiker AUGUSTUS DE MORGAN (1806 bis 1871), das hornersche Schema in vielen Artikeln beschrieb und ihm wohl letztlich auch seinen Namen gab.
WILLIAM GEORGE HORNER verstarb am 22. September 1837 in Bath, nachdem er kurz zuvor (und zwar nach dem Tode seines Sohnes) die Schule aufgegeben hatte.
Ruffini Zhu Shi-jie hornersches Schema Morgan algebraische Gleichungen Hornerschema Horner-Verfahren Chu Shih-Chieh ganzrationale Funktionen
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 