Funktionen mit der Gleichung y = f(x) = mx + n

Zusammenhänge, bei denen zwar ein gleichmäßiges (proportionales) Wachsen oder Abnehmen einer Größe erfolgt, der Ausgangswert aber von null verschieden ist, können durch Funktionen mit einer Gleichung der Form y = f(x) = mx + n beschrieben werden.

Beispiel 1: Eine Mietwagenfirma erhebt einen Grundbetrag von 50 Euro und dann für jeden Kilometer weitere 0,25 Euro.
Der für eine Fahrtstrecke von x Kilometern zu zahlende Betrag b (gemessen in Euro) ließe sich dann durch die Funktion
$b\left(x\right)=\mathrm{0,25}x+50\left(mitx\in \mathbb{N}\right)$
beschreiben.

Beispiel 2: Ein Speicher enthält $200m^3$ Wasser. Während der folgenden 24 Stunden fließen pro Stunde jeweils $3m^3$ Wasser zu und $\mathrm{4,5}{m}^3$ ab.
Den aktuellen Inhalt w (gemessen in $m^3$) nach t Stunden gibt dann die Funktion
$\begin{array}{c}w\left(t\right)=\left(3-\mathrm{4,5}\right)t+200\\ =-\mathrm{1,5}t+200\left(t=0;1;2;\mathrm{...};24\right)\end{array}$
an.

Beispiel 3: Die Betreiberfirma eines Handy-Netzes verlangt eine monatliche Grundgebühr von 10 Euro sowie für jede begonnene Minute eines Inlandgesprächs 2,8 Cent.
Der für ein Gesamtgesprächsdauer von t Minuten zu zahlende Monatsbetrag z (in Euro) wird in diesem Falle durch die Funktion
$z\left(t\right)=\mathrm{0,028}t+10\left(t\in \mathbb{N}\right)$
angegeben.

• Eine Funktion f mit einer Gleichung der Form
  $y=f\left(x\right)=mx+n\left(m,n\in ℝ\right)$
  oder einer Gleichung, die durch äquivalentes Umformen in diese Form überführt werden kann, heißt lineare Funktion.

Für lineare Funktionen ist der Definitionsbereich im Allgemeinen die Menge der reellen Zahlen (so nicht das mathematische oder das entsprechenden Anwendungsproblem einen Einschränkung verlangt), was dann auch für den Wertebereich $($ für $m\ne 0)$ gilt. Die Zahlen m und n sind Parameter.

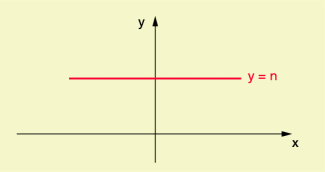
Eine Funktion der Form y = n, d.h. y = mx + n mit m = 0, heißt konstante Funktion. Der Graph einer konstanten Funktion mit
y = n ist eine Parallele zur x-Achse im Abstand n.

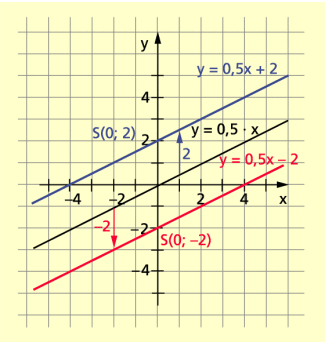
Für Funktionen mit der Gleichung y = f (x) = mx + n $\left(m,n\ne 0\right)$ gilt:

• Die Graphen bestehen aus Punkten, die auf einer Geraden liegen.
• n heißt absolutes Glied und gibt an, an welcher Stelle die Gerade die y-Achse schneidet.
• Bei gleichem Anstieg m und unterschiedlichem n sind die Graphen zueinander parallele Geraden.

Zeichnen der Graphen von Funktionen y = mx + n

Die einfachste Möglichkeit, den Graphen einer linearen Funktion zu zeichnen, ist das Verwenden von Werten aus einer Wertetabelle. Dabei sollte man leicht errechenbare Werte und im Interesse der Zeichengenauigkeit nicht zu nah beieinander liegende Werte verwenden.

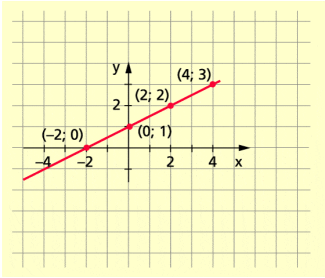
Beispiel 4:
Gleichung: y = 0,5x + 1

Wertetabelle:

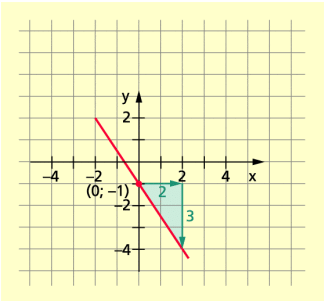
Man kann zum Zeichnen auch ein Steigungsdreieck und den Schnittpunkt mit der y-Achse (0; n) nutzen.

Beispiel 5:
Es ist der Graph der Funktion $y=-\frac{3}{2}x-1$ zu zeichnen.
Der Punkt (0; -1) ist der Schnittpunkt mit der y-Achse. Von diesem Punkt aus wird das Steigungsdreieck (um 2 Einheiten nach rechts und um 3 Einheiten nach unten) angetragen.

Nullstellenermittlung

Um die Nullstelle einer linearen Funktion zu ermitteln, wird in die Funktionsgleichung für y = 0 eingesetzt und die entstehende Bestimmungsgleichung nach x aufgelöst.

Beispiel 6:
Gesucht ist die Nullstelle der Funktion mit $y=\frac{3}{2}x-4.$
Es ist $0=\frac{3}{2}x-4$, also $4=\frac{3}{2}x$ und damit $\frac{8}{3}=x$.
Antwort: Die Nullstelle der Funktion ist $x_0=\frac{8}{3}.$