Definitionslücken

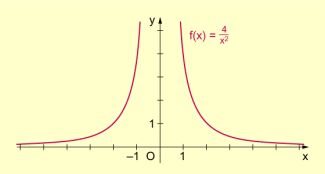
Bei links- und rechtsseitiger Annäherung an $x_0=0$ werden die Funktionswerte beliebig groß, d.h., für $x\to 0mitx<0$ gilt $f\left(x\right)\to +\infty$ und für $x\to 0mitx>0$ gilt ebenfalls $f\left(x\right)\to +\infty$. Die beiden „Äste“ des Graphen von f liegen auf derselben Seite der Abszissenachse.
Die Funktion f hat an der Stelle $x_0=0$ eine Polstelle ohne Vorzeichenwechsel.

• Beispiel 2: $\text{f(x)}=\frac{\text{1}}{\text{x}-\text{2}}$

Die Funktion besitzt an der Stelle $x_0=2$ eine Polstelle.
Die Gerade mit der Gleichung $x=2$ ist in diesem Fall Polgerade.
Nähert man sich der Polstelle von links $\left(x\to 2;x<2\right)$, dann werden die Funktionswerte beliebig klein $\left(f\left(x\right)\to -\infty \right)$. Bei Annäherung von rechts $\left(x\to 2;x>2\right)$ werden die Funktionswerte beliebig groß $\left(f\left(x\right)\to +\infty \right)$.
Die Funktion f hat an der Stelle $x=2$ eine Polstelle mit Vorzeichenwechsel.

• Ist $x_0$ Polstelle einer gebrochenrationalen Funktion f, so gilt:
  $f\left(x\right)\to +\infty bzw.f\left(x\right)\to -\infty fürx\to x_0$
  Die Gerade (Polgerade) mit der Gleichung $x=x_0$ nennt man auch senkrechte Asymptote des Graphen der Funktion f.

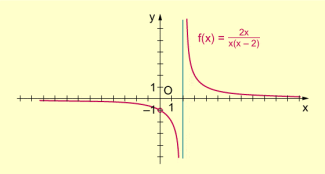
Der Punkt $\left(0;-1\right)$ gehört nicht zum Graphen der Funktion. Der Graph besteht aus zwei Hyperbelästen mit einem „Loch“. Kürzt man aus dem Funktionsterm den Faktor x (bzw. allgemein $x-x_0$), dann erhält man eine neue Funktion $\text{g(x)}=\frac{\text{2}}{\text{x}-\text{2}}$, die an der Stelle $x_0=0$ stetig ist.

Man sagt: Die Funktion f ist an der Stelle $x_0$ stetig fortsetzbar bzw. die Definitionslücke $x_0$ der Funktion f ist hebbar (Rechenbeispiel).

Anmerkungen: An der Stelle $x_1=2$ besitzt f (wie leicht nachprüfbar ist) eine Polstelle.

Die „Ersatzfunktion“ g kann auch in der folgenden Form geschrieben werden:
$g\left(x\right)=\{\begin{array}{cc}\frac{2}{x\cdot \left(x-2\right)}& fürx\ne 0\\ -1& fürx=0\end{array}$
Sie ist (im Gegensatz zu f) eine im gesamten Definitionsbereich stetige Funktion.