Monotonieverhalten von Funktionen

Im Folgenden soll der Zusammenhang zwischen Monotonie und 1. Ableitung untersucht werden.

Monotonie

#Analysis #Kurvendiskussion #monoton fallend #streng monoton #Monotonieverhalten #Krümmungsverhalten #oben beschränkt #unten beschränkt #obere schranke #untere schranke #streng monoton fallend #streng monoton wachsend

Eine Funktion f heißt in einem Intervall I ihres Definitionsbereichs $D_{f}$ genau dann monoton wachsend, wenn für beliebige $x_{1}, x_{2} \in I$ gilt:
$x_{1} < x_{2} \Rightarrow f (x_{1}) \leq f (x_{2})$
Eine Funktion f heißt in einem Intervall I ihres Definitionsbereichs $D_{f}$ genau dann monoton fallend, wenn für beliebige $x_{1}, x_{2} \in I$ gilt:
$x_{1} < x_{2} \Rightarrow f (x_{1}) \geq f (x_{2})$

Gilt für $x_{1} < x_{2}$ sogar $f (x_{1}) < f (x_{2}) b z w . f (x_{1}) > f (x_{2})$ , so nennt man f in dem Intervall I streng monoton wachsend bzw. streng monoton fallend.

Um eine Monotonieaussage über eine Funktion treffen zu können, reicht es nicht aus, nur für einige Argumente das Verhalten der Funktionswerte zu untersuchen werden – es muss vielmehr der gesamte Definitionsbereich bzw. das vorgegebene Intervall berücksichtigt werden. Man kann zu diesem Zweck prüfen, ob für positives h in einem bestimmten Intervall die Differenz $f (x + h) - f (x)$ größer oder kleiner als null ist. Im ersten Fall wäre f dann dort monoton wachsend, im zweiten Fall monoton fallend.

Es sind folgende Funktionen auf Monotonie zu untersuchen:

Beispiel 1: $f (x) = e^{x}; x \in R$

Monotonieverhalten einer Exponentialfunktion

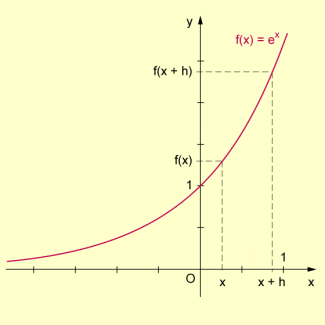
Es gilt: $f (x + h) - f (x)$ $= e^{x + h} - e^{x} = e^{x} (e^{h} - 1)$

Da $e^{x}$ stets positiv und auch $e^{h} - 1$ für h > 0 immer positiv ist, gilt $f (x + h) - f (x)$ > 0 für alle x. Die Funktion $f (x) = e^{x}; x \in R$ ist also (sogar streng) monoton wachsend.

Beispiel 2: $f (x) = \frac{1}{x}, x \in] 0; \infty [$

Monotonieverhalten einer Potenzfunktion

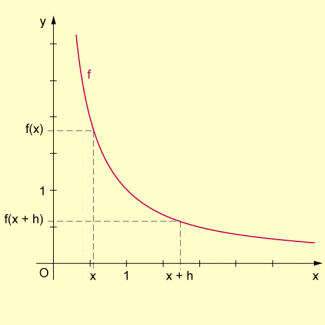
In diesem Falle gilt: $f (x + h) - f (x)$ $= \frac{1}{x + h} - \frac{1}{x} = \frac{x - x - h}{x (x + h)} = \frac{- h}{x (x + h)}$

Der als Resultat erhaltene Quotient ist im angegebenen Intervall für h > 0 stets negativ, die Funktion f dort also (streng) monoton fallend.

Der hier gewählte Untersuchungsweg kann bei komplizierteren Funktionstermen oder bei Wechsel des Monotonieverhaltens im Definitionsbereich freilich manchmal sehr aufwendig sein, wie das folgende Beispiel zeigt.

Beispiel 3: Die Funktion f mit $f (x) = x^{2} - 2 x - 1$ ist bezüglich Monotonie zu untersuchen.

Monotonieverhalten einer quadratischen Funktion

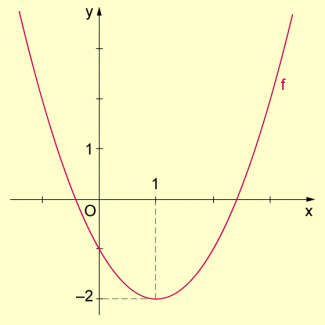
Anhand des Graphen gelangt man zwar schnell zu einer Vermutung (nämlich: f ist monoton fallend für x < 1 und monoton wachsend für x > 1), aber die zu oben analoge Rechnung führt zu dem folgenden Ausdruck, der schwerer zu diskutieren ist:
$\begin{matrix} f (x + h) - f (x) = {(x + h)}^{2} - 2 (x + h) - 1 - (x^{2} - 2 x - 1) \\ = 2 h x + h^{2} - 2 h \end{matrix}$

Eine einfachere Methode ergibt sich aus folgendem Satz zum Zusammenhang zwischen Monotonie und 1. Ableitung:

Eine im offenen Intervall differenzierbare Funktion f ist in diesem Intervall genau dann monoton wachsend (monoton fallend), wenn für alle $x \in I$ die Beziehung $f' (x) \geq 0$ (bzw. ) $f' (x) \leq 0$ gilt.

Der Beweis dieses Satzes muss wegen der „genau dann, wenn“-Aussage (also einer Äquivalenzaussage) „in beiden Richtungen“ geführt werden. Wir beschränken uns aber auf den Fall des monotonen Wachsens.

Beweisteil I

Voraussetzung:
f sei eine im offenen Intervall I differenzierbare Funktion und für alle $x \in I$ gelte $f' (x) \geq 0$ .

Behauptung:
f ist im Intervall I monoton wachsend (also: Für beliebige $x_{1}, x_{2} \in I$ mit $x_{1} < x_{2}$ gilt $f (x_{1}) \leq f (x_{2})$ ).

Beweis:

$x_{1}, x_{2} \in I$ seien beliebige Zahlen aus I. Dann gibt es zwischen ihnen nach dem Mittelwertsatz der Differenzialrechnung ein $x_{0} m i t f' (x_{0}) = \frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}}$ .
Wegen $x_{2} - x_{1} > 0 u n d f' (x_{0}) \geq 0$ gilt $f' (x_{0}) \cdot (x_{2} - x_{1}) = f (x_{2}) - f (x_{1}) \geq 0,$ d.h., es ist $f (x_{2}) \geq f (x_{1})$ für beliebige $x_{1}, x_{2} \in I$ .

Beweisteil II (in der „Gegenrichtung“)

Voraussetzung:
f ist im Intervall I differenzierbar und monoton wachsend (also: Für beliebige $x_{1}, x_{2} \in I$ mit $x_{1} < x_{2}$ gilt $f (x_{1}) \leq f (x_{2})$ ).

Behauptung:
Für alle $x \in I$ gilt $f' (x) \geq 0$ .

Beweis:

$x_{1}, x_{2} \in I$ mit $x_{1} < x_{2}$ seien beliebige Zahlen aus I. Dann gilt nach Voraussetzung $f (x_{1}) \leq f (x_{2})$ .
Wegen $x_{2} - x_{1} > 0 u n d f (x_{2}) - f (x_{1}) \geq 0$ ist der Quotient $\frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}} \geq 0$ und folglich auch sein Grenzwert für $x_{2} \to x_{1}$ . Da aber $x_{1}, x_{2}$ beliebige Zahlen aus I waren, gilt für alle $x \in I$ die Beziehung $f' (x) \geq 0$ . w. z. b. w.
Für monoton fallende Funktionen kann man den Beweis der entsprechenden Beziehung analog führen.

Anmerkungen:

Der obige Satz gibt eine Bedingung für die Monotonie einer Funktion an, die notwendig und hinreichend ist.
Wenn man im ersten Teil des Beweises f '(x) > 0 voraussetzt, so folgt stets $f (x_{2}) > f (x_{1})$ .
Der Beweis gilt also auch für strenge Monotonie. Der zweite Beweisteil ist hingegen für strenge Monotonie nicht allgemeingültig:
Wenn eine Funktion f streng monoton wachsend ist, dann müsste stets f '(x) > 0 gelten. Ein Gegenbeispiel dazu stellt die Funktion $f (x) = x^{3}$ dar, die zwar streng monoton wachsend ist, für die aber f '(0) = 0 gilt. Obiger Satz ist für strenge Monotonie folglich nur hinreichend.

Monotonieverhalten einer Potenzfunktion dritten Grades

Erneute Betrachtung der Beispiele

Unter Verwendung des oben bewiesenen Satzes lassen sich die eingangs genannten Funktionen leicht auf Monotonie untersuchen.

1) Für $f (x) = e^{x}; x \in R$ gilt $f' (x) = e^{x}$ . Da stets $e^{x}$ > 0 gilt, ist die Funktion f in ihrem gesamten Definitionsbereich streng monoton wachsend.

2) Die Funktion $f (x) = \frac{1}{x}, x \in] 0; \infty [$ hat die Ableitung $f' (x) = - \frac{1}{x^{2}}$ . Der Funktionsterm ist für alle x > 0 negativ und f demzufolge streng monoton fallend.

3) Die Ableitung von $f (x) = x^{2} - 2 x - 1$ , $x \in R$ ist $f' (x) = 2 x - 2$ .
Der Funktionsterm ist positiv für x > 1 und negativ für x < 1. In diesen Teilbereichen ist damit die Funktion f streng monoton wachsend bzw. streng monoton fallend.

Graph einer quadratischen Funktion und ihrer Ableitung

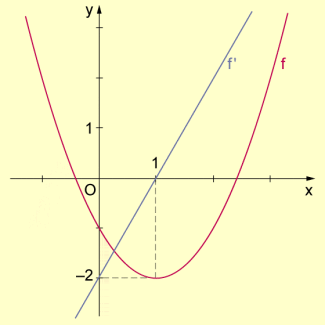
Der angegebene Satz lässt sich beispielsweise auch für den Nachweis bestimmter Ungleichheitsbeziehungen verwenden. Um etwa nachzuweisen, dass für $0 < x < \frac{π}{2}$ stets $x < \tan x$ gilt, betrachten wir die Funktion $f (x) = x - \tan x$ . Wegen

$f' (x) = 1 - (1 + \tan^{2} x) = - \tan^{2} x < 0$

ist f im Intervall $0 < x < \frac{π}{2}$ streng monoton fallend. Da f(0) = 0 ist, gilt für $0 < x < \frac{π}{2}$ die Beziehung $f (x) = x - \tan x$ < 0 und damit $x < \tan x$ .

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel