Extremwertprobleme beim senkrechten Wurf
In der Mechanik werden u.a. Bewegungsvorgänge von Körpern untersucht. Dabei wird in der Regel nach dem zurückgelegten Weg, der Geschwindigkeit und der Beschleunigung gefragt. Insbesondere bei den Wurfbewegungen lassen sich viele Fragestellungen mithilfe der Methoden der Differenzialrechnung bearbeiten.
Beim senkrechten Wurf nach oben geht man davon aus, dass ein Körper mit einer bestimmten Anfangsgeschwindigkeit senkrecht nach oben „geschossen“ wird. Anschließend wird untersucht, wie er sich im Schwerefeld der Erde bewegt.
Mithilfe der 1. Ableitung lassen sich Aussagen über die Momentangeschwindigkeit oder die maximale Steighöhe gewinnen.
-

Karl Holzhauser - MEV Verlag, Augsburg
Unter der Voraussetzung, dass
- die Luftreibung vernachlässigt wird,
- der Körper idealisiert als Massepunkt betrachtet wird und
- die Bewegungsvorgänge hinreichend nahe an der Erdoberfläche ablaufen und somit die Fallbeschleunigung konstant bleibt,
lautet das Ort-Zeit-Gesetz (auch Weg-Zeit-Gesetz genannt) für den senkrechten Wurf nach oben:
Dabei sind
y - die von der Abwurfstelle gemessene Höhe des Wurfkörpers;
- die Anfangsgeschwindigkeit des Wurfkörpers;
g - die Fallbeschleunigung;
t - die Zeit.
Beim Ort-Zeit-Gesetz handelt es sich um eine Funktion die von t abhängt:
Die maximale Steighöhe , die ein mit abgeworfener Körper erreichen kann, erhält man als Extremum der Funktion y(t).
Dieses findet man mithilfe der 1. Ableitung der Funktion y(t). Man erhält:
(Diese Formel beschreibt die Geschwindigkeit des Körpers in Abhängigkeit von der Zeit. Man kann also auch schreiben
Die Nullstelle der 1. Ableitung erhält man aus der Gleichung
. Sie lautet:
Anschaulich ist dieser Ausdruck die sogenannte Steigzeit des Körpers, d. h., die Zeit, die der Körper bis zum Erreichen des höchsten Punktes benötigt. Rechnerisch hat man also die Nullstelle der „Geschwindigkeitsfunktion“ bestimmt, somit also die Zeit ermittelt, nach der der Körper die Geschwindigkeit null hat.)
Dass an der Extremstelle ein lokales Maximum vorliegt, verdeutlicht die 2. Ableitung , die für jedes t negativ ist.
(Der Graph der Funktion ist eine nach unten geöffnete Parabel, so dass die Art des Extremums auch ohne die Untersuchung der 2. Ableitung eindeutig bestimmt werden kann.)
-
Weg-Zeit-Diagramm eines senkrechten Wurfs nach oben
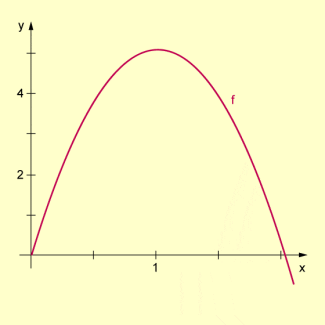
Die maximale Steighöhe erhält man, wenn man die Extremstelle in die Ausgangsgleichung einsetzt:
Daraus ergibt sich folgende Interpretationsmöglichkeit:
Die Steighöhe ist umso größer, je größer die Anfangsgeschwindigkeit bzw. je kleiner die Fallbeschleunigung ist.

