- Lexikon
- Mathematik Abitur
- 6 Differenzialrechnung
- 6.1 Grundbegriffe der Differenzialrechnung
- 6.1.1 Ableitung einer Funktion
- Grafisches Differenzieren
Grafisches Differenzieren
Der Anstieg der Tangente an den Graphen einer Funktion im Punkt kann mithilfe einer Zeichnung näherungsweise bestimmt werden. Damit erhält man sofort einen Näherungswert für die Ableitung der Funktion an der Stelle .
Ein derartiges Verfahren zum Bestimmen der Ableitung an einer Stelle heißt zeichnerisches oder grafisches Differenzieren.
- Beispiel: Für die Sinusfunktion soll die Ableitung an den Stellen grafisch ermittelt werden.
Schrittfolge zur Lösung:
1. Die Funktion wird im Intervall grafisch dargestellt.
2. An den vorgegebenen Stellen werden die Tangenten an den Funktionsgraphen gezeichnet.
3. Mithilfe von Anstiegsdreiecken wird der Anstieg an den einzelnen Stellen abgelesen.
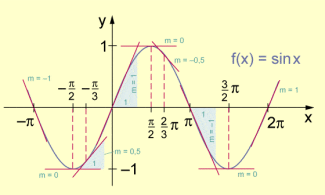
Graph der Sinusfunktion mit Tangenten und Anstiegsdreiecken
Die folgende Tabelle enthält für die ausgewählten Stellen die zugeordneten zeichnerisch ermittelten Ableitungswerte :
Diese Tabelle kann als Wertetabelle einer neuen Funktion aufgefasst werden. Sie ist dadurch entstanden, dass den Stellen der Funktion f mit ihre Ableitung zugeordnet wurde. Diese Zuordnung stellt wieder eine Funktion dar und heißt Ableitungsfunktion der Funktion f.
Sind keine Missverständnisse zu befürchten, so spricht man auch kurz von Ableitung anstelle von Ableitungsfunktion. Man muss aber stets bedenken, dass begrifflich zwischen Ableitung an einer Stelle als einer reellen Zahl und der Ableitung als einer neuen Funktion zu unterscheiden ist.
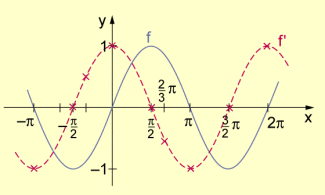
Die Ableitungsfunktion der Funktion kann nun mithilfe der Wertetabelle dargestellt werden. Der Verlauf lässt vermuten, dass für die Ableitungsfunktion der Sinusfunktion gilt.
Die Graphen der Sinusfunktion und ihrer Ableitungsfunktion
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 