Ableitung von Funktionen in Parameterdarstellung
Funktionen können in unterschiedlicher Form gegeben sein. Eine der Möglichkeiten ist die Darstellung in Parameterform. Hierbei werden die Variablen x und y aus der Funktionsgleichung y = f(x) unter Verwendung einer Hilfsvariablen, eines Parameters, z.B. t, ausgedrückt. Das heißt also: x = und y = .
Es gilt: Eine in Parameterdarstellung gegebene Funktion y = f(x) mit x = und y = ist differenzierbar, wenn die Ableitungen von und nach t existieren und .
Die Ableitungsfunktion lautet dann f'(x) = .
Beweis:
Aus und erhält man .
Anmerkung: Um die Ableitung nach dem Parameter t von der Ableitung nach x in zu unterscheiden, werden Ableitungen nach dem Parameter t häufig nicht mit einem nachgestellten Strich, sondern durch einen Punkt über den betreffenden Variablen gekennzeichnet. Es gilt also:
Beispiel
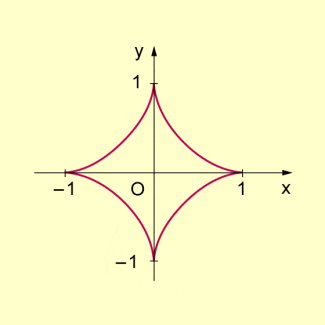
Die Parameterdarstellung einer Astroide lautet
;
.
Die Ableitungen sind dann:
;
Daraus ergibt sich:
Dieser Quotient ist t für und nicht definiert, was in Übereinstimmung mit dem Kurvenverlauf steht: Die Astroide hat in den Punkten (0; 1), (0; –1), (1; 0) und (–1; 0) „Spitzen“, sie ist dort nicht differenzierbar.
Für die zweite Ableitung y'' = f''(x) = einer in Parameterdarstellung gegebenen Funktion y = f(x) mit x = und y = gilt (in Kurzform geschrieben):
(sofern )
-
Astroide