Konstantenregel der Differenzialrechnung

Wir vermuten das Folgende: Eine konstante Funktion $f (x) = c (c \in ℝ, a b e r f e s t)$ besitzt für alle $x \in ℝ$ die Ableitung $f^{'} (x) = 0.$

Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
Viel günstiger als andere Nachhilfe und schützt deine Daten.

Jetzt 30 Tage risikofrei testen

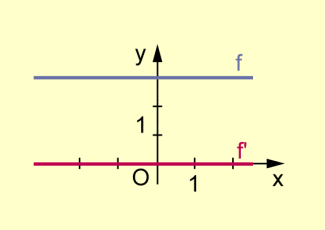
Wir betrachten die konstante Funktion $f (x) = c$ für alle $x \in ℝ$ .
Ihr Graph ist eine Parallele zur x-Achse.

Zum Nachweis dieser Vermutung wird der Differenzenquotient für eine beliebige Stelle $x_{0} \in D_{f}$ gebildet:
$\begin{matrix} d (h) = \frac{f (x_{0} + h) - f (x)}{h} \\ = \frac{c - c}{h} = \frac{0}{h} = 0 (f ü r h \neq 0) \end{matrix}$

Also gilt auch:

$f^{'} (x_{0}) = \lim_{h \to 0} 0 = 0$

Damit gilt allgemein die Konstantenregel der Differenzialrechnung:

Eine konstante Funktion $f (x) = c (c \in ℝ, a b e r f e s t)$ besitzt für alle $x \in ℝ$ die Ableitung $f^{'} (x) = 0$ .

Anmerkung: Bei der Ableitung einer Funktion ist stets genau zu beachten, welche der (u.U. mehreren) in der Funktionsgleichung auftretenden Variablen die unabhängige (Funktions-)Variable kennzeichnet.

Beispielsweise ist für $f (x) = c$ nach obiger Regel die Ableitung $f^{'} (x) = 0$ , während dies für $f (c) = c (c \in ℝ)$ nicht zutrifft.

Lernhelfer (Duden Learnattack GmbH): "Konstantenregel der Differenzialrechnung." In: Lernhelfer (Duden Learnattack GmbH). URL: http://www.lernhelfer.de/schuelerlexikon/mathematik-abitur/artikel/konstantenregel-der-differenzialrechnung (Abgerufen: 25. April 2025, 02:13 UTC)

Suche nach passenden Schlagwörtern

Jetzt durchstarten

Entspannt durch die Schule mit KI-Tutor Kim und Duden Learnattack.

Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
Viel günstiger als andere Nachhilfe und schützt deine Daten.

Verwandte Artikel

Partielle Ableitungen

Für eine Funktion mit einer Gleichung $y = f (x)$ , also für eine Funktion mit genau einer unabhängigen Variablen x, ist die erste Ableitung $y' = f' (x_{0})$ an einer Stelle $x_{0}$ erklärt durch den Grenzwert des Differenzenquotienten an dieser Stelle:
$f' (x_{0}) = \lim_{h \to 0} \frac{f (x_{0} + h) - f (x_{0})}{h}$

Interpretiert man diesen Grenzwert geometrisch, so gibt er den Anstieg der Tangente an den Graphen von f im Punkte $P_{0} (x_{0}; f (x_{0}))$ an.

Es sei nun $z = f (x, y)$ die Gleichung einer Funktion f mit zwei unabhängigen Variablen x und y. Betrachtet man diese Funktion für ein konstantes $y = y_{0}$ , so erhält man eine Funktion $z = f (x, y_{0})$ mit nunmehr nur einer unabhängigen Variablen x, für die man wie oben angegeben den Grenzwert des Differenzenquotienten an einer Stelle $x_{0}$ aufstellen kann. Existiert dieser Grenzwert, so nennt man ihn die partielle Ableitung erster Ordnung der Ausgangsfunktion $z = f (x, y)$ nach x an der Stelle $(x_{0}; y_{0})$ und schreibt:
$f_{x} (x_{0}; y_{0}) = \lim_{h \to 0} \frac{f (x_{0} + h, y_{0}) - f (x_{0}, y_{0})}{h}$

Kettenregel der Differenzialrechnung

Im Folgenden soll die Kettenregel der Differenzialrechnung bewiesen werden.
Die Kettenregel besagt: Die Ableitung einer verketteten Funktion ist gleich dem Produkt der Ableitungen von äußerer und innerer Funktion an der jeweiligen Stelle.
Für die Anwendung der Kettenregel ist eine auf der leibnizschen Schreibweise $\frac{d y}{d x}$ anstelle von $f' (x)$ beruhende Notation sehr einprägsam.

Ableitung von Potenzfunktionen

Unter einer Potenzfunktion wird eine Funktion mit einer Gleichung der Form $y = f (x) = x^{n} (x \in ℝ; n \in ℤ \ {0})$ verstanden.

Ihre Ableitung erfolgt mithilfe der Potenzregel der Differenzialrechnung:

Die Funktion $f (x) = x^{n} (n \in ℕ; n \geq 1)$ ist differenzierbar und $f^{'} (x) = n \cdot x^{n - 1}$ gilt.

Potenzregel der Differenzialrechnung

Im Folgenden soll die Potenzregel der Differenzialrechnung für Potenzfunktionen $f (x) = x^{n}$ bewiesen werden.
Über die natürlichen Zahlen als Exponenten hinaus ist die Potenzregel auf Potenzfunktionen mit ganzzahligen Exponenten n $(f a l l s x_{0} \neq 0)$ , mit rationalen Exponenten n $(x > 0)$ und sogar mit reellen Exponenten n $(x > 0)$ anwendbar. Man nennt diesen Sachverhalt auch die erweiterte Potenzregel.

Produktregel der Differenzialrechnung

Im Folgenden soll die Produktregel der Differenzialrechnung bewiesen werden.
Die Produktregel lässt sich auch auf endlich viele Faktoren erweitern.

Konstantenregel der Differenzialrechnung

Schule wird easy mit KI-Tutor Kim und Duden Learnattack

Suche nach passenden Schlagwörtern