Partielle Ableitungen

Für eine Funktion mit einer Gleichung $y = f (x)$ , also für eine Funktion mit genau einer unabhängigen Variablen x, ist die erste Ableitung $y' = f' (x_{0})$ an einer Stelle $x_{0}$ erklärt durch den Grenzwert des Differenzenquotienten an dieser Stelle:
$f' (x_{0}) = \lim_{h \to 0} \frac{f (x_{0} + h) - f (x_{0})}{h}$

Interpretiert man diesen Grenzwert geometrisch, so gibt er den Anstieg der Tangente an den Graphen von f im Punkte $P_{0} (x_{0}; f (x_{0}))$ an.

Es sei nun $z = f (x, y)$ die Gleichung einer Funktion f mit zwei unabhängigen Variablen x und y. Betrachtet man diese Funktion für ein konstantes $y = y_{0}$ , so erhält man eine Funktion $z = f (x, y_{0})$ mit nunmehr nur einer unabhängigen Variablen x, für die man wie oben angegeben den Grenzwert des Differenzenquotienten an einer Stelle $x_{0}$ aufstellen kann. Existiert dieser Grenzwert, so nennt man ihn die partielle Ableitung erster Ordnung der Ausgangsfunktion $z = f (x, y)$ nach x an der Stelle $(x_{0}; y_{0})$ und schreibt:
$f_{x} (x_{0}; y_{0}) = \lim_{h \to 0} \frac{f (x_{0} + h, y_{0}) - f (x_{0}, y_{0})}{h}$

Verschachtelte Funktionen integrieren

#Analysis #Integralrechnung #Verschachtelte Funktionen #Verschachtelung #Faktorregel #Integration #Integrationsgrenzen #Substitution #partielle Integration #bestimmtes Integral #unbestimmtes Integral #Stammfunktion #Funktionsscharen

Betrachtet man analog die Funktion f für ein konstantes $x = x_{0}$ , so erhält man jetzt eine Funktion $z = f (x_{0}, y)$ mit der unabhängigen Variablen y. Den Grenzwert
$f_{y} (x_{0}; y_{0}) = \lim_{k \to 0} \frac{f (x_{0}, y_{0} + k) - f (x_{0}, y_{0})}{k}$
nennt man ihn die partielle Ableitung erster Ordnung der Ausgangsfunktion $z = f (x, y)$ nach y an der Stelle $(x_{0}; y_{0})$ .

Zusammenfassung:
Ist eine Funktion $z = f (x, y)$ für ein konstantes $y = y_{0}$ an einer Stelle $x_{0}$ differenzierbar, so heißt $z = f (x, y)$ dort partiell nach x differenzierbar. Die dazugehörige Ableitung $f_{x} (x_{0}, y_{0})$ wird partielle Ableitung von f nach x an der Stelle $(x_{0}; y_{0})$ genannt.
Entsprechend heißt die Funktion partiell nach y differenzierbar, wenn sie für ein konstantes $x = x_{0}$ an einer Stelle $y_{0}$ nach y differenzierbar ist. Die dazugehörige Ableitung $f_{y} (x_{0}, y_{0})$ wird partielle Ableitung von f nach y an der Stelle $(x_{0}; y_{0})$ genannt.

Anmerkungen:
Ist die Funktion $z = f (x, y)$ für jedes x bzw. y des Definitionsbereichs partiell nach x bzw. y differenzierbar, so spricht man schlechthin von den partiellen Ableitungen nach x bzw. y und schreibt $f_{x} (x, y)$ bzw. $f_{y} (x, y)$ .
In Analogie zu $f' (x) = \frac{d f (x)}{d x}$ schreibt man für $f_{x} (x, y)$ bzw. $f_{y} (x, y)$ auch $f_{x} (x, y) = \frac{\partial f (x, y)}{\partial x} b z w . f_{y} (x, y) = \frac{\partial f (x, y)}{\partial y}$
und spricht von der partiellen Ableitung von f nach x bzw. von f nach y.

Für die Bildung der partiellen Ableitungen erster Ordnung lassen sich sämtliche Ableitungsregeln einer Funktion mit einer unabhängigen Variablen übertragen, wenn man jeweils beachtet, welche Variable im betreffenden Zusammenhang die unabhängige ist.

Beispiel 1: Gesucht sind die partiellen Ableitungen der Funktion
$z = f (x; y) = 2 x^{3} - 4 x^{2} y + 7 x y^{2} + 4 y^{3}$
y wird als konstant angesehen: $f_{x} (x, y) = 6 x^{2} - 8 x y + 7 y^{2}$
x wird als konstant angesehen: $f_{y} (x, y) = - 4 x^{2} + 14 x y + 12 y^{2}$

Beispiel 2: Gesucht sind die partiellen Ableitungen der Funktion
$z = f (x; y) = x^{y} (x, y > 0)$
y wird als konstant angesehen – wir erhalten eine Potenzfunktion: $f_{x} (x, y) = y x^{y - 1}$
x wird als konstant angesehen – wir erhalten eine Exponentialfunktion: $f_{y} (x, y) = x^{y} \cdot \ln x$ .

Geometrische Deutung der partiellen Ableitung

Eine Funktion $z = f (x, y)$ von zwei Variablen beschreibt im Allgemeinen eine Fläche im Raum.

Geometrische Deutung der partiellen Ableitung

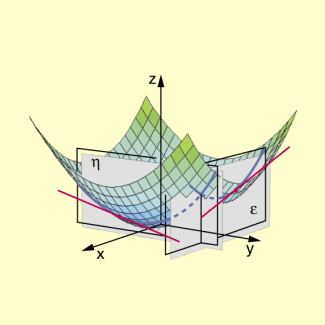
Durch die Annahme $y = y_{0} = k o n s t .$ werden alle die Punkte der betreffenden Fläche herausgegriffen, die zugleich in der zur xz-Ebene parallelen Ebene $ε$ mit $y = y_{0} = k o n s t .$ liegen. Diese Punkte bilden eine Kurve $f (x, y_{0})$ , die als Schnittkurve der Ebene $ε$ und der Fläche $z = f (x, y)$ gedeutet werden kann. Der Anstieg der Tangente an diese Schnittkurve wird durch die partielle Ableitung $f_{x} (x, y)$ beschrieben. Entsprechend liefert die Annahme $x = x_{0} = k o n s t .$ eine zur yz-Ebene $η$ parallele Ebene, welche die Fläche $z = f (x, y)$ in der Kurve $f (x_{0}, y)$ schneidet. Die partielle Ableitung $f_{y} (x, y)$ gibt den Anstieg der Tangente an diese Schnittkurve an.

Beispiel 3: Der Graph der Funktion $z = f (x, y) = x^{2} + y^{2}$ stellt ein Rotationsparaboloid dar. Es entsteht durch Rotation der Parabel $y = x^{2}$ um die z-Achse.

Geometrische Deutung der partiellen Ableitung am Beispiel (Rotationsparaboloid)

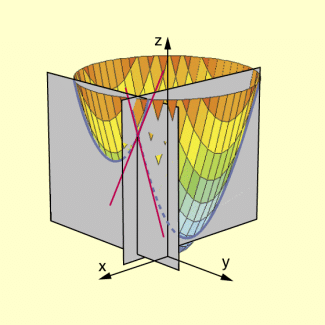
Die partiellen Ableitungen lauten: $f_{x} (x, y) = 2 x; f_{y} (x, y) = 2 y$
Mit ihrer Hilfe kann man nun die Anstiege der Tangenten in einem Punkt $P_{0}$ berechnen.
So erhält man für $P_{0} (1; 2; z_{0})$ die partiellen Ableitungen
$f x ( 1 , 2 ) = 2 und f y ( 1 , 2 ) = 4$ .
Die im Punkt $P_{0}$ zur xz-Ebene parallele Tangente hat also einen Anstieg von 2, die im selben Punkt zur yz-Ebene parallele Tangente hat den Anstieg 4.

Gradientenvektor

Die partiellen Ableitungen erster Ordnung einer Funktion fasst man im sogenannten Gradientenvektor zusammen und schreibt
$g r a d (f (x, y)) = (\begin{matrix} f_{x} \\ f_{y} \end{matrix})$ .
Für obiges Beispiel des Rotationsparaboloids würde der Gradientenvektor also folgendermaßen lauten
$g r a d (f (x, y)) = (\begin{matrix} 2 x + y^{2} \\ x^{2} + 2 y \end{matrix})$

Der Gradientenvektor ordnet somit jeder Stelle $(x_{0}; y_{0})$ des Definitionsbereichs von $z = f (x, y)$ einen Vektor zu, der folgende Eigenschaften besitzt:

Ausgehend vom Punkt $(x_{0}; y_{0})$ zeigt der Gradientenvektor in Richtung des steilsten Anstiegs in der Fläche $z = f (x, y)$ .
Der durch den Gradientenvektor beschriebene Vektor ( Gradient ) steht senkrecht auf der durch $(x_{0}; y_{0})$ verlaufenden Höhenlinie von $z = f (x, y)$ .
Der Betrag des Gradienten ist der Wert der Steigung in Gradientenrichtung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel

Partielle Ableitungen

Verschachtelte Funktionen integrieren

Geometrische Deutung der partiellen Ableitung

Gradientenvektor

Rechtliches

Einloggen