Ableitung einer Funktion

Eine Kurve hat nicht immer nur eine rein geometrische Bedeutung. Oft beschreibt man damit die Abhängigkeit zweier (etwa physikalischer) Größen.

Ein Beispiel dafür ist das Geschwindigkeit-Zeit-Diagramm einer beschleunigten Bewegung.

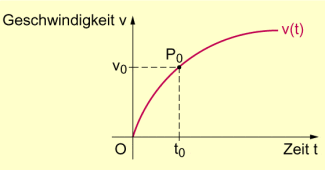
Der Kurvensteigung (im Punkt $P_0$) entspricht physikalisch die Zunahme der Geschwindigkeit (in $P_0$), also die Beschleunigung.

Wenn wir die Kurvensteigung ermitteln, so berechnen wir in Wirklichkeit die physikalische Größe Beschleunigung. Deshalb ist es notwendig, dem Begriff der Kurvensteigung einen allgemeineren Namen zu geben.

Anstatt Kurvensteigung in $P_0$ sagt man Ableitung in $P_0$ oder Differenzialquotient in $P_0$.

Der Begriff Ableitung

Existiert an der Stelle $x_0$ des Definitionsbereiches einer reellen Funktion f der Grenzwert des Differenzenquotientens
$\frac{f\left(x_0+h\right)-f\left(x_0\right)}{h}bzw.\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$
für x gegen $x_0$, so wird dieser als Ableitung oder Differenzialquotient der Funktion f an der Stelle $x_0$ bezeichnet. Die Funktion f heißt dann an der Stelle $x_0$ differenzierbar.
Die Ableitung von f an der Stelle $x_0$ bezeichnet man mit $f^{\prime }\left(x_0\right)$ und schreibt folgendermaßen:
$f^{\prime }\left(x_0\right)=\underset{h\to 0}{\lim }\frac{f\left(x_0+h\right)-f\left(x_0\right)}{h}bzw.f^{\prime }\left(x_0\right)=\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$

Andere Bezeichnungen sind
${\frac{df(x)}{dx}|}_{x_0}bzw.{\frac{dy}{dx}|}_{x_0}bzw.{y^{\prime }|}_{x_0}$.

Geometrisch gesehen gibt die Ableitung einer Funktion die Steigung (der Anstieg) der Tangente (bzw. des Funktionsgraphen) an der Stelle $x_0$ an, da der Differenzenquotient die Steigung der Sekante durch die Punkte $P\left(x;f\left(x\right)\right)$ und $P_0\left(x_0;f\left(x_0\right)\right)$ angibt.

• Beispiel 1:
  Für die Funktion $f(x)=x^{2}mitx\in ℝ$ erhält man an einer beliebigen Stelle $x_0$:
  $\begin{array}{l}{f}^{\prime }\left(x_0\right)=\underset{h\to 0}{\lim }\frac{{\left(x_0+h\right)}^2-x_0{}^2}{h}\\ =\underset{h\to 0}{\lim }\frac{2x_{0}h+h^2}{h}=\underset{h\to 0}{\lim }\left(2x_0+h\right)=2x_0\end{array}$
  Für $x_0=1$ erhält man für die Tangente im Punkt $P_0(1;1)$ den Anstieg $f^{\prime }(1)=2$ und damit die Tangentengleichung $f_t(x)-1=2(x-1)$, also $f_t(x)=2x-1$.
   
• Beispiel 2:
  Für die Betragsfunktion $f(x)=\left|x\right|$ gilt:
  $\frac{f(x)-f(0)}{x-0}=\frac{\left|x\right|}{x}=\{\begin{array}{c}1fürx>0\\ -1fürx<0\end{array}$
  Das heißt, der Grenzwert $\underset{x\to 0}{\lim }\frac{\left|x\right|}{x}$ existiert nicht. Die Betragsfunktion ist an der Stelle $x_0=0$ nicht differenzierbar.

Anmerkung: Bei komplizierten Termstrukturen verwendet man zum Bilden der Ableitung zweckmäßigerweise einen GTA.

Praktische Anwendungen

Bei praktischen Anwendungen des Differenzialquotienten bedeutet die Ableitung $f^{\prime }(x_0)$ oft die lokale oder punktuelle Änderungsrate.

• Beispiel 3:
  Bewegungsvorgänge lassen sich durch eine Weg-Zeit-Funktion $s(t)$ beschreiben. Der Differenzenquotient
  $\frac{s(t)-s(t_0)}{t-t_0}$
  der Weg-Zeit-Funktion gibt die mittlere Geschwindigkeit und damit die mittlere Änderungsrate der Weglänge bezüglich des Zeitintervalls $\left[t_0;t\right]$ an. Der Grenzwert
  $\underset{t\to t_0}{\lim }\frac{s(t)-s(t_0)}{t-t_0}$
  (also die Ableitung der Weg-Zeit-Funktion an der Stelle $t_0$), heißt Momentangeschwindigkeit zum Zeitpunkt $t_0$, sie beschreibt die lokale oder punktuelle Änderungsrate der Weglänge bezüglich der Zeit.

Anmerkung: Ableitungen nach der Zeit werden in der Physik statt mit dem Ableitungsstrich mit einem Punkt bezeichnet, beispielsweise ist $\dot{s}(t)$ die Ableitung von $s(t)$ nach der Zeit.

Weitere Anwendungsbeispiele für Änderungsraten sind mit der Steuerfunktion, der Kostenfunktion sowie in vielfältigen naturwissenschaftlichen Zusammenhängen (z.B. radioaktiver Zerfall, chemische Reaktionen, Temperaturgefälle, Luftdruckgefälle) gegeben.