Dreiecksarten

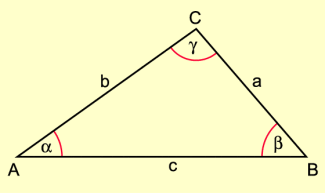
Ein Dreieck ist ein geschlossener Streckenzug aus drei Strecken. Die drei Strecken sind die Seiten des Dreiecks. Je zwei Seiten haben einen Eckpunkt gemeinsam (Bild 1).
Die Eckpunkte des Dreiecks werden mit Großbuchstaben (z. B. A, B, C) bezeichnet. Üblicherweise erfolgt die Bezeichnung entgegen dem Uhrzeigersinn (im positiven Drehsinn).
Die Dreieckseiten werden mit Kleinbuchstaben (z. B. a, b, c) entsprechend den gegenüberliegenden Eckpunkten bezeichnet.

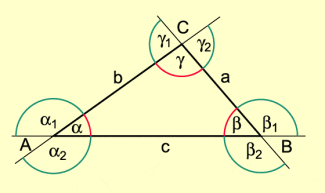
Die Winkel im Inneren des Dreiecks werden Innenwinkel genannt und zumeist mit kleinen griechischen Buchstaben bezeichnet $\left(z.B.\alpha ,\beta ,\gamma \right).$
Die Nebenwinkel der Innenwinkel sind die Außenwinkel des Dreiecks (Bild 2).

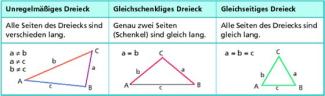
Dreiecke lassen sich nach den Längen der Seiten in unregelmäßige, gleichschenklige oder gleichseitige Dreiecke einteilen (Bild 3).
In einem gleichschenkligen Dreieck sind die Schenkel die beiden gleich langen Seiten. Der gemeinsame Eckpunkt der Schenkel ist die Spitze des Dreiecks. Die dritte Seite des gleichschenkligen Dreiecks heißt Grundseite oder Basis. Die beiden der Basis anliegenden, gleich großen Winkel heißen Basiswinkel.
In einem gleichseitigen Dreieck beträgt die Größe jedes Innenwinkel $60°$, jedes Außenwinkel $120°$.

.

Betrachtet man die Innenwinkel der Dreiecke, so unterscheidet man spitzwinklige, rechtwinklige und stumpfwinklige Dreiecke (Bild 4).

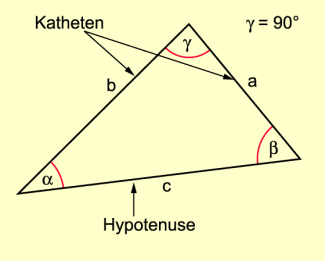
Ein Dreieck heißt rechtwinklig, wenn ein Winkel $90°$beträgt (Bild 5). Die dem rechten Winkel gegenüberliegende Seite heißt Hypotenuse. Die beiden anderen Seiten, die Schenkel des rechten Winkels, nennt man Katheten. Die an der Hypotenuse anliegenden Winkel sind komplementär, d. h., die Summe dieser beiden Winkel beträgt $90°$.