- Lexikon
- Mathematik
- 7 Planimetrie
- 7.6 Dreiecke
- 7.6.1 Dreiecksarten
- Dreiecksungleichung, Beweis
Dreiecksungleichung, Beweis
Bei der Konstruktion von Dreiecken (und Vierecken) spielen neben den Kongruenzsätzen weitere allgemeine Gesetzmäßigkeiten eine Rolle, zum Beispiel die folgenden:
- In einem Dreieck liegt der längeren (kürzeren) Seite stets der größere (kleinere) Winkel gegenüber.
- Durch die Angabe von zwei bzw. drei Winkeln ist ein Dreieck zwar noch nicht eindeutig bestimmt, aber alle Dreiecke dieser Art sind zueinander ähnlich (formgleich).
- In einem Dreieck ist die Summe zweier Seitenlängen stets größer als die Länge der dritten Seite.
Der zuletzt angeführte Sachverhalt ist die sogenannte Dreiecksungleichung, für die wegen ihrer Bedeutsamkeit im Folgenden ein Beweis angegeben werden soll.
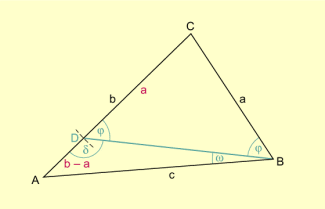
| Nebenstehende Figur macht zunächst anschaulich einsichtig, dass der Weg von A über C nach B länger ist als der direkte Weg von A nach B. Das heißt, liegen drei Punkte A, B und C nicht auf einer Geraden, so gilt: |
|
Wir beweisen nun die Dreiecksungleichung.
Für die Seitenlängen a, b und c eines Dreiecks mit (ohne Beschränkung der Allgemeinheit)
ist dabei zu zeigen, dass gilt. Das heißt, zu zeigen ist:
Für gibt es einen Punkt D zwischen A und C mit (obiges Bild). Für die Winkelgrößen gilt dann
,
da jeder Innenwinkel eines Dreiecks stets kleiner ist als jeder der nicht anliegenden Außenwinkel (Außenwinkelsatz).
Da dem größeren Winkel stets die größere Seite gegenüberliegt, gilt also (im Dreieck ABD):
Für den Fall folgt analog auch . Gilt aber , so ist trivialerweise erfüllt.
Damit ist die Dreiecksungleichung bewiesen und kann in Kurzfassung folgendermaßen formuliert werden:
Die Summe zweier Dreiecksseiten ist stets größer als die dritte Seite.
Wir betrachten dazu folgendes Beispiel:
Man konstruiere ein Dreieck ABC mit .
Zunächst entsteht der Eindruck, dass das Dreieck ABC nach dem Kongruenzsatz sss eindeutig bestimmt sei.
Zeichnet man nun zuerst , dann ist der Punkt C durch Kreise um A mit und B mit bestimmt. Diese schneiden sich in diesem Fall aber nicht. Folglich gibt es kein Dreieck mit vorgegebenen Seitenlängen, da sie die Dreiecksungleichungen nicht erfüllen. Zwar ist a + c > b (2,4 cm + 4,4 cm > 1,8 cm) und
b + c > a (1,8 cm + 4,4 cm > 2,4 cm), aber es gilt nicht
b + a > c (denn 1,8 cm + 2,4 cm < 2,4 cm).
Anmerkung: Wenn man feststellen will, ob man ein Dreieck mit den drei vorgegebenen Seitenlängen a, b und c zeichnen kann, so bietet sich folgendes einfaches Verfahren an:
Man ordnet a, b und c der Größe nach. Ist dann etwa , so braucht man nur zu prüfen, ob ist. Nur in diesem Fall existiert das entsprechende Dreieck, denn mit gilt und wegen ist auch .
Beweisfigur zur Dreiecksungleichung
Ein Angebot von 