Kongruenzabbildungen
Eine Kongruenzabbildung (Bewegung) ist eine umkehrbar eindeutige Abbildung der einen Figur auf eine andere Figur .
Zwei Figuren und sind zueinander kongruent (deckungsgleich) genau dann, wenn sie die gleiche Form und Größe haben.
Schreibweise:
Kongruente Figuren lassen sich durch eine Verschiebung, eine Spiegelung, eine Drehung oder eine Zusammensetzung von ihnen aufeinander abbilden.
Eine Kongruenzabbildung (Bewegung) ist eine umkehrbar eindeutige Abbildung der einen Figur auf eine andere Figur .
Zwei Figuren und sind zueinander kongruent (deckungsgleich) genau dann, wenn sie die gleiche Form und Größe haben.
Schreibweise:
Kongruente Figuren lassen sich durch eine Spiegelung, eine Verschiebung eine Drehung oder eine Zusammensetzung von ihnen aufeinander abbilden. Die Spiegelung (Geradenspiegelung) ist die grundlegende Kongruenzabbildung, da sich alle anderen Bewegungen durch Nacheinanderausführen von Spiegelungen ersetzen lassen.
Kongruenzabbildungen werden durch folgende Merkmale charakterisiert:
- Das Bild einer Geraden ist stets wieder eine Gerade
(Geradentreue). - Die Bilder paralleler Geraden sind zueinander parallele Geraden
(Parallelentreue). - Das Bild eines Winkels ist stets ein Winkel der gleichen Größe
(Winkeltreue). - Das Bild eines Kreises ist stets ein Kreis
(Kreisverwandtschaft). - Das Bild einer Strecke ist stets eine Strecke gleicher Länge
(Längentreue).
Zur Charakterisierung der Eigenschaften einer Bewegung ist die Frage nach Fixpunkten, Fixgeraden und deren Lage von besonderem Interesse.
Jeder Punkt A, der bei einer Bewegung auf sich selbst abgebildet wird, heißt Fixpunkt bezüglich der Bewegung.
Jede Gerade g, die bei einer Bewegung auf sich selbst abgebildet wird, heißt Fixgerade bezüglich der Bewegung.
Wird die Gerade g sogar Punkt für Punkt auf sich selbst abgebildet, d. h., wird jeder Punkt der Geraden auf sich selbst abgebildet, heißt die Gerade Fixpunktgerade bezüglich der Bewegung.
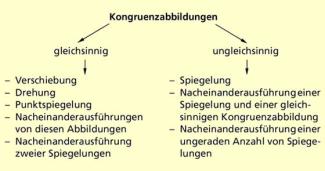
Kongruenzabbildungen lassen sich in gleichsinnige (z. B. Verschiebung, Drehung, Punktspiegelung) und ungleichsinnige (z. B. Geradenspiegelung) Kongruenzabbildungen unterteilen (Bild 2).
-
Übersicht über Kongruenzabbildungen