Kosinussatz

Der Kosinussatz gehört neben dem Sinussatz zu den wichtigsten Sätzen der Trigonometrie. Der Kosinussatz drückt eine Beziehung zwischen den drei Seiten und einem Winkel im Dreieck aus.
Man kann aus zwei Seiten und dem von ihnen eingeschlossenen Winkel die dritte Seite berechnen oder aus drei Seiten einen Winkel.

Der Kosinussatz gehört neben dem Sinussatz zu den wichtigsten Sätzen der Trigonometrie. Der Kosinussatz drückt eine Beziehung zwischen den drei Seiten und einem Winkel im Dreieck aus.
Man kann auch aus zwei Seiten und dem von ihnen eingeschlossenen Winkel die dritte Seite berechnen oder aus drei Seiten einen Winkel.

Kosinussatz

In jedem Dreieck ist das Quadrat über einer Seite gleich der Summe der Quadrate über den beiden anderen Seiten vermindert um das doppelte Produkt aus diesen Seiten und dem Kosinus des von ihnen eingeschlossenen Winkels:

$\begin{array}{l} a^{2} = b^{2} + c^{2} - 2 b c \cdot \cos α \\ b^{2} = a^{2} + c^{2} - 2 a c \cdot \cos β \\ c^{2} = a^{2} + b^{2} - 2 a b \cdot \cos γ \end{array}$

Kosinussatz am spitzwinkligen Dreieck

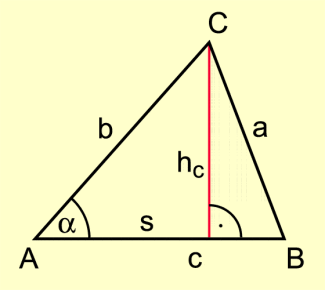
Mithilfe des Satzes von Pythagoras lässt sich der Kosinussatz herleiten (Bild 2):

$h_{b} = a \cdot \sin γ$ und $d = b - a \cdot \cos γ$

$\begin{array}{l} c^{2} = h_{b}^{2} + d^{2} \\ c^{2} = a^{2} \cdot \sin^{2} γ + b^{2} - 2 b a \cdot \cos γ + a^{2} \cos^{2} γ \\ c^{2} = a^{2} (\sin^{2} γ + \cos^{2} γ) + b^{2} - 2 a b \cdot \cos γ \\ c^{2} = a^{2} + b^{2} - 2 a b \cdot \cos γ \end{array}$

Der Satz des Pythagoras ist ein Spezialfall des Kosinussatzes, denn für $γ = 90 °$ und somit cos 90° = 0 ergibt sich:
$c^{2} = a^{2} + b^{2}$

Herleitung Kosinussatz

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel

Kosinussatz

Rechtliches

Einloggen