Dreieckskonstruktion

Die Konstruktion von Dreiecken ist anhand sogenannter Bestimmungsstücke mithilfe von Zirkel und Lineal durchführbar. Man unterteilt die Dreieckskonstruktionen in Konstruktionen aus Seiten und Winkeln (Grundkonstruktionen) und in Konstruktionen, bei denen auch weitere Bestimmungsstücke wie Höhen, Winkelhalbierende gegeben sind.

Dreiecke konstruieren

#Dreieck #Dreieckskonstruktion #Dreiecke konstruieren #planfigur #Konstruktionsplan #Höhe #Winkelhalbierende #Mittelsenkrechte #Lot

Die Konstruktion von Dreiecken ist anhand sogenannter Bestimmungsstücke mithilfe von Zirkel und Lineal durchführbar. Man unterteilt die Dreieckskonstruktionen in Konstruktionen aus Seiten und Winkeln (Grundkonstruktionen) und in Konstruktionen, bei denen auch weitere Bestimmungsstücke wie Höhen, Winkelhalbierende gegeben sind.

Alle Konstruktionen, bei denen die in den Kongruenzsätzen genannten Stücke vorgegeben sind, können eindeutig ausgeführt werden, falls die Vorgaben der Dreiecksungleichungen, der Innenwinkelsatz und die Beziehung zwischen Seiten und Innenwinkeln des Dreiecks erfüllt sind.

Konstruktion nach dem Kongruenzsatz sss

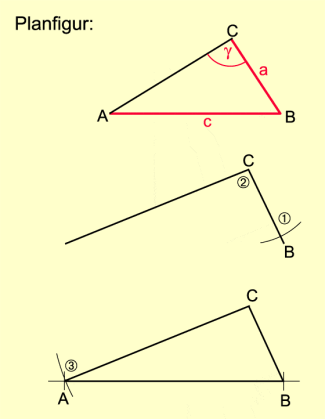
Gegeben sind die Längen der drei Dreiecksseiten (Bild 1).
Konstruktionsbeschreibung:

Auf einer Geraden wird die Strecke AB mit $\bar{A B}$ = c abgetragen.
Um A wird ein Kreisbogen mit dem Radius b und um B wird ein Kreisbogen mit dem Radius a gezeichnet.
Die Schnittpunkte der Kreisbogen sind $C_{1}$ und $C_{2}$ . Unter Beachtung der Orientierung werden die Punkte A und B mit C ( $C_{1}$ ) zum Dreieck ABC verbunden.

Konstruktion nach sss

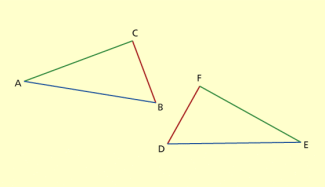
Konstruktion nach dem Kongruenzsatz wsw

Gegeben sind die Seitenlänge c und die Größen der anliegenden Winkel $α$ und $β$ (Bild 2).

Konstruktionsbeschreibung:

Auf einer Geraden wird die Strecke AB mit $\bar{A B}$ = c abgetragen.
Im Punkt A wird an die Strecke AB der Winkel $α$ und im Punkt B an die Strecke AB der Winkel $β$ angetragen.
Der Schnittpunkt der freien Schenkel von $α$ und $β$ ist der Punkt C. Die Punkte A und B werden mit C zum Dreieck ABC verbunden.

Konstruktion nach wsw

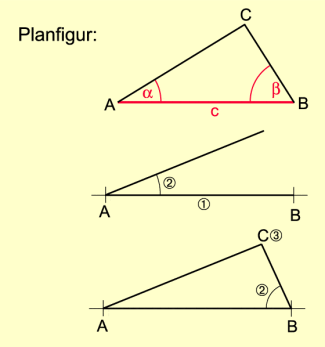
Konstruktion nach dem Kongruenzsatz sws

Gegeben sind die Seitenlängen b und c sowie die Größe des Winkels $α$ (Bild 3).

Konstruktionsbeschreibung:

Auf einer Geraden wird die Strecke AB mit $\bar{A B}$ = c abgetragen.
Im Punkt A wird an die Strecke AB der Winkel $α$ angetragen.
Um A wird ein Kreisbogen mit dem Radius b gezeichnet. Er schneidet den freien Schenkel des Winkels $α$ im Punkt C. Der Punkt C wird mit A bzw. B zum Dreieck ABC verbunden.

Konstruktion nach sws

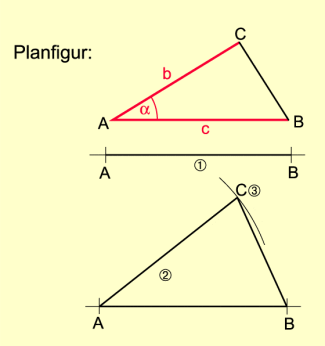
Konstruktion nach dem Kongruenzsatz SsW

Gegeben sind die Streckenlängen a und c sowie die Größe des Winkels $γ$ , welcher der größeren Seite gegenüberliegt (Bild 4).

Konstruktionsbeschreibung:

Auf einer Geraden wird die Strecke BC mit $\bar{B C}$ = a abgetragen.
Im Punkt C wird an die Strecke CB der Winkel $γ$ angetragen.
Um B wird ein Kreisbogen mit dem Radius c gezeichnet. Er schneidet den freien Schenkel des Winkels $γ$ im Punkt A. Der Punkt B wird mit A zum Dreieck ABC verbunden.

Übersicht über die Konstruktion von Dreiecken mithilfe der Kongruenzsätze

Bild

Konstruktion nach SsW

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel

Dreieckskonstruktion

Dreiecke konstruieren

Konstruktion nach dem Kongruenzsatz sss

Konstruktion nach dem Kongruenzsatz wsw

Konstruktion nach dem Kongruenzsatz sws

Konstruktion nach dem Kongruenzsatz SsW

Übersicht über die Konstruktion von Dreiecken mithilfe der Kongruenzsätze

Rechtliches

Einloggen