Drehung
Eine Drehung um einen Punkt Z mit dem Drehwinkel ist eine eineindeutige Abbildung der Ebene auf sich selbst, bei der für das Bild P' jedes Punktes P gilt:
- P' liegt auf dem Kreis um Z durch P.
- (P'ZP) =
Drehung
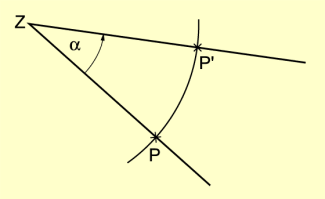
Der Punkt Z wird Drehpunkt oder Drehzentrum genannt. Z ist Fixpunkt bei einer Drehung.
Drehungen erfolgen – wenn nicht anders angegeben – entgegengesetzt zum Uhrzeigersinn (positiver Drehsinn).
Drehung
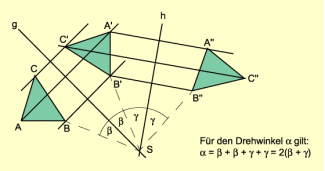
Eine Drehung lässt sich als Doppelspiegelung an zwei Geraden g und h darstellen, wobei g und h einander im Drehzentrum (Drehpunkt) Z schneiden.
Doppelspiegelung an einander schneidenden Geraden
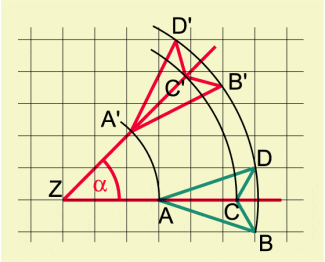
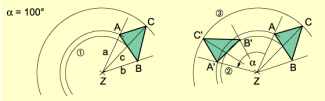
Konstruktion des Bildes eines Dreiecks bei Drehung um Z
Konstruktionsbeschreibung:
- Es werden Strahlen a, b, c mit dem Anfangspunkt Z durch A, B, C und Kreisbögen mit dem Mittelpunkt Z durch A, B, C gezeichnet.
- Im Punkt Z wird an jeden der Strahlen a, b und c der Winkel unter Berücksichtigung seiner Orientierung angetragen.
- A' liegt auf dem Kreisbogen durch A sowie auf dem zweiten Schenkel des Winkels . Entsprechend werden B' und C' konstruiert, und die Punkte A', B' und C' werden miteinander verbunden.
Konstruktion einer Drehung
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 