Ähnlichkeit von Figuren

Eine Figur $F_2$ heißt ähnlich zur Figur $F_1$, wenn sie durch eine maßstäbliche Vergrößerung oder Verkleinerung aus $F_1$ hervorgegangen ist. Das konstante Verhältnis der einander entsprechenden Strecken heißt Ähnlichkeitsfaktor k. Schreibweise: $F_2~F_1$

Ähnliche Figuren haben also die gleiche Form, unterscheiden sich aber im Allgemeinen in der Größe. Die entsprechenden Winkel und Streckenverhältnisse sind gleich.

Für ähnliche Figuren gelten folgende Beziehungen:

• Jede Figur ist zu sich selbst ähnlich $\left(F_1~F_1\right)$.
• Aus $F_1~F_2$ folgt stets $F_2~F_1$.
• Aus $F_1~F_2$ und $F_2~F_3$ folgt $F_1~F_3$.

Ist $F_2$ ähnlich zu $F_1$ mit dem Ähnlichkeitsfaktor k, so ist auch $F_1$ ähnlich zu $F_2$, jedoch mit dem Ähnlichkeitsfaktor $\frac{1}{k}$.

Eine Vergrößerung bzw. Verkleinerung mit dem Ähnlichkeitsfaktor k = 1 ist eine identische Abbildung (eine kongruente Abbildung).
Bei maßstäblichen Vergrößerungen bzw. Verkleinerungen müssen alle Streckenlängen im gleichen Verhältnis vergrößert bzw. verkleinert werden.

Wichtige Sätze der Geometrie lassen sich mithilfe der Ähnlichkeit beweisen, so z. B. Sätze aus der Satzgruppe des Pythagoras oder Sätze am Kreis.

Beispiel:
Behauptung:
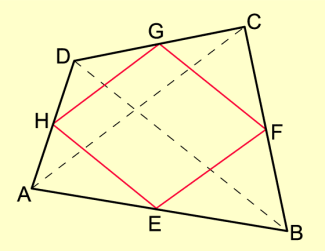
Die Mittelpunkte der Seiten eines beliebigen Vierecks bilden die Eckpunkte eines Parallelogramms.

Beweisidee:
Die Punkte E, F, G und H seien die Mittelpunkte der Seiten des Vierecks.
Die Strecke AC erhält man aus EF bzw. aus GH durch die zentrische Streckung $Z_1\text{ bzw}\text{. }{Z}_2$ mit B bzw. D als Streckungszentrum und k = 2.
Es gilt also $EF\parallel AC\text{ und }GH\parallel AC,\text{ woraus EF}\parallel \text{GH}$ folgt.
Aus $\overline{AC}=2\cdot \overline{EF}=2\cdot \overline{GH}\text{ folgt }\overline{\text{EF}}=\overline{GH}$.
EF und GH sind also zu einander parallel und gleich lang.