Streckenteilung
Mithilfe der Strahlensätze kann eine Strecke durch Konstruktion in einem beliebigen rationalen Verhältnis geteilt bzw. mit einem beliebigen rationalen Faktor vervielfacht werden.
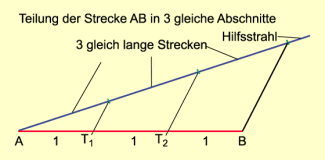
1. Teilen einer Strecke AB in n gleiche Teile (Bild 1)
Im Punkt A der Strecke wird ein Strahl (Hilfsstrahl) angetragen. Auf diesem Strahl wird von A aus eine beliebige Strecke n-mal mit dem Zirkel abgetragen. Der letzte Endpunkt der abgetragenen Strecken wird mit dem Punkt B der zu teilenden Strecke verbunden. Eine Parallelverschiebung durch die Endpunkte der Strecken auf dem Hilfsstrahl ergibt die gesuchten Teilungspunkte auf der Strecke AB.
Teilung einer Strecke AB in n gleiche Teile
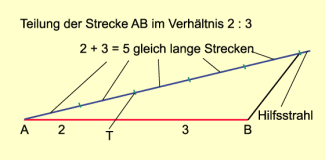
2. Teilen einer Strecke AB im Verhältnis p : q (Bild 2)
Im Punkt A der Strecke wird ein Strahl (Hilfsstrahl) angetragen. Auf diesem Strahl wird von A aus eine beliebige Strecke (p + q)-mal mit dem Zirkel abgetragen. Der letzte Endpunkt der abgetragenen Strecken wird mit dem Punkt B der zu teilenden Strecke verbunden. Eine Parallelverschiebung durch den p-ten Endpunkt der Strecken auf dem Hilfsstrahl ergibt den gesuchten Teilungspunkt auf der Strecke AB.
Teilen einer Strecke AB im Verhältnis p : q
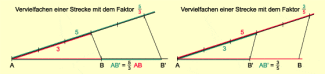
3. Vervielfachen einer Strecke AB mit dem Faktor (Bild 3)
Im Punkt A der Strecke wird ein Strahl (Hilfsstrahl) angetragen. Auf diesem Strahl wird von A aus eine beliebige Strecke n-mal mit dem Zirkel abgetragen. Der letzte Endpunkt der abgetragenen Strecken wird mit dem Punkt B der zu vervielfachenden Strecke verbunden. Auf dem Hilfsstrahl wird von A aus z-mal die gleiche Strecke abgetragen. Eine Parallelverschiebung durch den z-ten Endpunkt der Strecken auf dem Hilfsstrahl ergibt den gesuchten Punkt auf der Strecke AB bzw. auf der Verlängerung von AB.
Vervielfachen einer Strecke
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 