Maßstäblich Darstellen

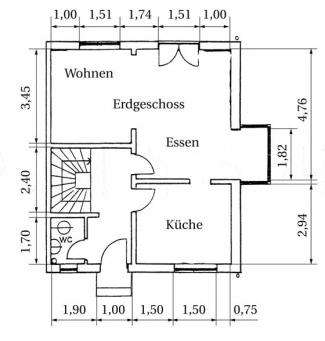
Viele Familien gehen beim Neueinrichten von Zimmern so vor, dass sie den Grundriss des Zimmers genau ausmessen, einen geeigneten Maßstab wählen und die Angaben auf ein Blatt Papier übertragen. In diesen Grundriss werden Tür und Fenster eingezeichnet. Nun kann man die Grundrisse aller Möbel in diesem Raum im gleichen Maßstab zeichnen und ausschneiden (Bild 1). Die Modelle für die Möbel werden auf der Skizze solange angeordnet, bis man mit der Gestaltung des Zimmers zufrieden ist.

Möbelhäuser bieten die Gestaltung von Räumen mithilfe von Computern als Service an. Die Originalmaße werden automatisch verkleinert dargestellt. Der Kunde sieht z. B. seine Küche teilweise sogar räumlich komplett vor sich. Die entsprechende Software kann man auch für seinen PC zu Hause kaufen.

In zahlreichen Berufen gehört das maßstäbliche Verkleinern oder Vergrößern von Vorlagen mithilfe von Computern oder Pantografen zu den wichtigsten Tätigkeiten. Architekten entwerfen ganze Häuser am Reißbrett. Alle Vorgaben wie z. B. Fenster, Türen, elektrische Anschlüsse müssen exakt maßstäblich in die Zeichnungen eingetragen werden (Bild 2).

Archäologen übertragen ihre Fundorte auf maßstabsgetreue Zeichnungen und zeichnen in diese Abbildungen die Lage jedes Fundstücks ein. Dazu wird über die Ausgrabungsstelle ein Rahmen mit einem Gitternetz gelegt. Parallel wird auf einer verkleinerten Zeichnung die Lage jedes Fundstücks in einer Art Koordinatensystem markiert.

Goldschmiede übertragen Schriftzüge verkleinert auf Ringe oder Pokale. Auch die Beschriftung von Kugelschreibern erfolgt über eine Verkleinerung eines vorgegebenen Schriftzuges.

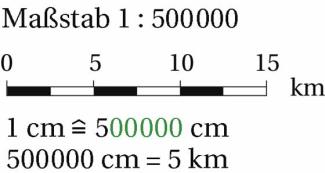
Landkarten sind immer maßstäbliche Verkleinerungen. Die erste Zahl gibt die Länge auf der Karte (Bildlänge) an. Die zweite Zahl gibt die Länge in der Wirklichkeit (Originallänge) an. Wie genau eine Karte ist, wird durch ihren Maßstab bestimmt (Bild 3).