Funktionsgraphen und Punkte

Ein Auto soll für die Untersuchung des Kraftstoffverbrauchs eine Teststrecke während 6 min möglichst genau mit einer Geschwindigkeit von 90 km/h (also 1,5 km/min) durchfahren.
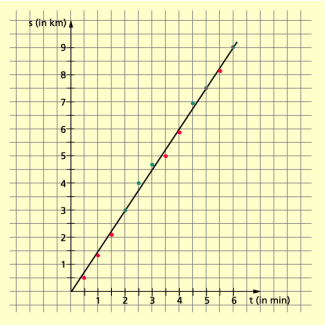
Die zugehörige Funktion f mit der Gleichung $s=f\left(t\right)=\mathrm{1,5}t$ (t in Minuten, s in Kilometer) besitzt den in Bild 1 dargestellten Graphen.

Auf einem Messgerät werden im Abstand von 0,5 min Zahlenpaare angegeben, in denen das erste Element die vergangene Fahrtzeit und das zweite den bis dahin zurückgelegten Weg bedeutet:
$\begin{array}{l}\{\left(0;0\right),\left(\mathrm{0,5};\mathrm{0,5}\right),\left(1;\mathrm{1,4}\right),\left(\mathrm{1,5};\mathrm{2,2}\right),\left(2;3\right),\left(\mathrm{2,5};4\right),\left(3;\mathrm{4,7}\right),\\ \left(\mathrm{3,5};5\right),\left(4;\mathrm{5,9}\right),\left(\mathrm{4,5};\mathrm{6,9}\right),\left(5;\mathrm{7,5}\right),\left(\mathrm{5,5};\mathrm{8,2}\right),\left(6;9\right)\}\end{array}$
Wir können feststellen: Liegt der einem Wertepaar entsprechende Punkt $P_1\left(s_1;t_1\right)$
– unterhalb des Graphen von $s=f\left(t\right)$, ist also $s_1<f\left(t_1\right)$, so ist die bis dahin zurückgelegte Strecke im Vergleich zu den Zielwerten zu klein;
– oberhalb des Graphen von $s=f\left(t\right)$, ist also $s_1>f\left(t_1\right)$, so ist die bis dahin zurückgelegte Strecke im Vergleich zu den Zielwerten zu groß.
Dann und nur dann, wenn $P_1$ auf dem Graphen von f liegt, wenn also $s_1=f\left(t_1\right)$ ist, befindet sich das Auto bezüglich seiner Geschwindigkeit genau „im Limit“.

Verallgemeinert formuliert:

Ein Punkt $P_1\left(x_1;y_1\right)$ liegt genau dann auf dem Graphen der Funktion $y=f\left(x\right)$, wenn $y_1=f\left(x_1\right)$ist, d. h., wenn die Koordinaten $x_1$, $y_1$ von $P_1$ die Gleichung $y=f\left(x\right)$ erfüllen.
(Gilt dagegen $y_1>f\left(x_1\right)$ oder $y_1<f\left(x_1\right)$, erfüllt also $\left(x_1;y_1\right)$ die Gleichung $y=f\left(x\right)$ nicht, so liegt der Punkt $P_1\left(x_1;y_1\right)$ – wenn man in Richtung der y-Achse blickt – „oberhalb“ bzw. „unterhalb“ des Graphen von f).

Von besonderem Interesse sind die Punkte des Graphen einer Funktion f, in denen dieser
– die x-Achse schneidet (oder berührt),
– die y-Achse schneidet.

Der Schnittpunkt $P_x$ des Graphen einer Funktion $y=f\left(x\right)$ mit der x-Achse hat die Koordinaten (x; 0). Das Zahlenpaar (x; 0)muss also die Gleichung $y=f\left(x\right)$ erfüllen, d. h., es muss gelten:
f(x) = 0

Die aus dieser Gleichung ermittelte Abszisse des Schnittpunkts des Graphen von f mit der x-Achse nennt man eine Nullstelle von f.

Beispiel: $y=f\left(x\right)=3x-9$
Wir setzen y = 0. Aus 0 = 3x – 9 erhalten wir:
3x = 9 bzw. x = 3

Das heißt: x = 3 ist die Nullstelle der Funktion f und $P_x\left(3;0\right)$ ist der Schnittpunkt des Graphen von f mit der x-Achse.
Anmerkung: Der Graph einer Funktion $y=f\left(x\right)$ kann die x-Achse mehrfach schneiden oder berühren.

Der Schnittpunkt $P_y$ des Graphen einer Funktion $y=f\left(x\right)$ mit der y-Achse hat die Koordinaten (0; y). Das Zahlenpaar (0; y) muss also die Gleichung $y=f\left(x\right)$ erfüllen, d. h., es muss gelten:
y = f(0)

Setzt man also in der Funktionsgleichung $y=f\left(x\right)$ für x die Zahl 0 ein, so erhält man die Ordinate y des Schnittpunkts des Graphen von f mit der y-Achse.

Beispiel: $y=f\left(x\right)=3x-9$
Wir setzen für x = 0 und erhalten:
y = 3 · 0 – 9 bzw. y = –9
Das heißt:
Der Graph von f schneidet die y-Achse im Punkt $P_y\left(0;-9\right)$.
Anmerkung: Der Graph einer Funktion $y=f\left(x\right)$ kann die y-Achse wegen der notwendigen Eindeutigkeit der Zuordnung $x\to f\left(x\right)$  höchstens einmal schneiden.

Wir verdeutlichen die obigen Zusammenhänge und Begriffe noch einmal an einem zusammenfassenden Beispiel.

Beispiel:
Gegeben ist eine Funktion f mit der Gleichung $y=f\left(x\right)=\mathrm{0,5}{x}^2-\mathrm{4,5}$.
a) Es ist zu untersuchen, ob die Punkte $P_1\left(1;-4\right),P_2\left(-2;-\mathrm{2,5}\right)bzw.P_3\left(2;\mathrm{2,5}\right)$ auf dem Graphen von f liegen.
b) Es sind die Schnittpunkte des Graphen mit den Koordinatenachsen zu ermitteln.

Lösung zu a)
Wir setzen nacheinander die Koordinaten der gegebenen Punkte in die Gleichung von f ein und untersuchen die entstehenden Gleichheitsaussagen:
$\begin{array}{l}{P}_1:-4=\mathrm{0,5}\cdot 1^2-\mathrm{4,5}=-4(wahreAussage)\\ P_2:-2=\mathrm{0,5}\cdot {\left(-2\right)}^2-\mathrm{4,5}=-2(wahreAussage)\\ P_3:\mathrm{2,5}=\mathrm{0,5}\cdot 2^2-\mathrm{4,5}=-\mathrm{2,5}(falscheAussage)\end{array}$
$P_{1}und{P}_2$ liegen also auf dem Graphen von f, $P_3$ liegt nicht auf dem Graphen.

Lösung zu b)
– Schnittpunkt mit der x-Achse:
Wir setzen y = 0. Aus 0 = 0,5x² –4,5 erhalten wir:
0,5x² = 4,5 bzw. x² = 9

Durch Wurzelziehen ergibt sich:
$x_1=3bzw.x_2=-3$
Das heißt: $x_1=3und{x}_2=-3$ sind die Nullstellen der Funktion f, $P_1\left(3;0\right)und{P}_2\left(-3;0\right)$ sind die Schnittpunkte des Graphen von f mit der x-Achse.

– Schnittpunkt mit der y-Achse:
Wir setzen x = 0 und erhalten:
y =0,5 · 0² – 4,5 = –4,5
Das heißt: Der Graph von f schneidet die y-Achse im Punkt $P_y\left(0;-\mathrm{4,5}\right)$.