Gerade und ungerade Funktionen

Eine Funktion f heißt gerade Funktion, wenn mit x auch (–x) zu ihrem Definitionsbereich gehört und für alle Argumente x gilt:
  f ( −   x ) = f ( x )
Eine Funktion f heißt ungerade Funktion, wenn mit x auch (–-x) zu ihrem Definitionsbereich gehört und für alle Argumente x gilt:
  f ( −   x ) = −   f ( x )

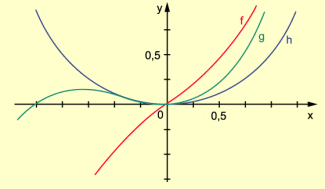
Wir untersuchen die Graphen der Funktionen y = f   ( x ) = x 2 und y = g   ( x ) = 1 2 x 3 auf Symmetrieeigenschaften.
Anhand Bild 1 lässt sich feststellen:

  1. Der Graph von f liegt symmetrisch zur y-Achse.

    Das heißt:
    • Argumente, die sich lediglich in ihrem Vorzeichen unterscheiden, besitzen den gleichen Funktionswert.
    • Punkte des Graphen, deren Abszissen lediglich entgegengesetztes Vorzeichen besitzen, haben die gleiche Ordinate.
       
  2. Der Graph von g liegt punktsymmetrisch zum Koordinatenursprung O.

    Das heißt:
    • Argumente, die sich lediglich in ihrem Vorzeichen unterscheiden, besitzen entgegengesetzte Funktionswerte (besitzen Funktionswerte, die sich ebenfalls allein in den Vorzeichen unterscheiden).
    • Punkte des Graphen, deren Abszissen lediglich entgegengesetztes Vorzeichen besitzen, haben entgegengesetzte Ordinaten (haben Ordinaten, die sich ebenfalls allein in den Vorzeichen unterscheiden).

Diese Eigenschaften führen zu einer weiteren Einteilungsmöglichkeit für Funktionen, wobei aber dadurch nicht alle Funktionen erfasst werden:

  • Eine Funktion f heißt gerade Funktion, wenn mit x auch
    (–x) zu ihrem Definitionsbereich gehört und für alle Argumente x gilt:
      f ( −   x ) = f ( x )
  • Eine Funktion f heißt ungerade Funktion, wenn mit x auch (–x) zu ihrem Definitionsbereich gehört und für alle Argumente x gilt:
      f ( −   x ) = −   f ( x )
Beispiel einer geraden und ungeraden Funktion

Beispiel einer geraden und ungeraden Funktion

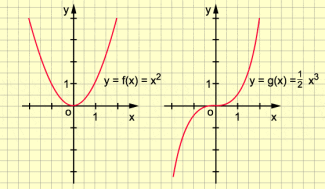
Gerade und ungerade Funktionen sowie ihre Graphen besitzen die oben für die speziellen Funktionen f bzw. g ermittelten Eigenschaften.

Will man untersuchen, ob bestimmte durch ihre Gleichungen gegebenen Funktionen gerade oder ungerade sind, so kann man zu einer ersten Vermutung anhand der Graphen dieser Funktionen gelangen. Für eine exakte rechnerische Untersuchung vergleicht man die Funktionswerte   f   ( x ) und   f   ( −   x ) (mit x ,     − x ∈ D ).

Beispiel:
Es ist zu untersuchen, welche der Funktionen f, g bzw. h mit
  y = f   ( x ) = x 3 +     x   y = g   ( x ) = x 3 +     x 2   y = h   ( x ) = 1 2 x 4 +     1 2 x 2
gerade oder ungerade sind.
In Bild 2 sind f, g und h grafisch dargestellt.

Rechnerische Untersuchung:

  • f   ( −   x ) = ( −   x ) 3 + ( −   x ) = −   x 3 − x = f   ( −   x )
    f ist eine ungerade Funktion.
     
  • g   ( −   x ) = ( −   x ) 3 + ( −   x ) 2 = −   x 3 +     x 2
    Da der Funktionsterm −   x 3 +     x 2 weder mit g   ( x ) noch mit g   ( −   x ) übereinstimmt, ist g weder eine gerade noch eine ungerade Funktion.
     
  • h   ( −   x ) = 1 2 ( −   x ) 4 +     1 2 ( −   x ) 2 = 1 2 x 4 +     1 2 x 2 = h   ( x )
    h ist eine gerade Funktion.
Untersuchung von speziellen Funktionen

Untersuchung von speziellen Funktionen

gerade Funktion interaktiv Funktion ungerade Funktion ungerade Mathcad zentralsymmetrisch gerade axialsymmetrisch Berechnungsbeispiel achsensymmetrisch Symmetrie symmetrisch Graph Rechenbeispiel punktsymmetrisch
Lexikon Share
Mathe Note verbessern?
 

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

  • 40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
  • Hausaufgabenhilfe per WhatsApp
  • Original Klassenarbeiten mit Lösungen
  • Deine eigene Lern-Statistik
  • Kostenfreie Basismitgliedschaft
Mathe kostenlos lernen
Verwandte Artikel
alle anzeigen
Angaben zum Lexikon
Impressum
© Duden Learnattack GmbH, 2024

Einloggen