Intervallschachtelung
Beim Bestimmen der Lösung einer Gleichung mittels Intervallschachtelung wird das Intervall so verkleinert, dass die Nullstelle der entsprechenden Funktion in dem verkleinerten Intervall liegt. Dieses Vorgehen wird wiederholt, bis das Intervall so klein ist, dass ein Wert aus dem Intervall als hinreichend genaue Näherung für die Nullstelle betrachtet werden kann.
Bei der Bestimmung der Lösung einer Gleichung mittels Intervallschachtelung wird das Intervall so verkleinert, dass die Nullstelle der entsprechenden Funktion in dem verkleinerten Intervall liegt.
Das Verfahren der schrittweisen Annäherung an die Lösung einer Gleichung gehört zu den Iterationsverfahren.
Von einem Iterationsverfahren spricht man, wenn man aus einer Näherungslösung durch Anwendung eines Algorithmus zu einer besseren Näherungslösung und letztlich die Lösung prinzipiell beliebig gut an die exakte Lösung heranführen kann. Man sagt dann, dass die Iteration konvergiert.
Grundgedanke der Näherungsverfahren zum Bestimmen der Lösungen von Gleichungen ist, die Gleichung in eine Funktion umzuwandeln, sodass die Variable der Gleichung als Veränderliche der Funktion erscheint. Es werden dann die Nullstellen dieser Funktion gesucht. Statt der Gleichung p(x) = 0 wird die Funktion f(x) = p(x) betrachtet.
Dabei muss die Funktion folgende Bedingungen erfüllen:
- Der Graph der Funktion kann über dem Intervall in einem Zug gezeichnet werden (stetig).
- Die Funktionswerte am Anfang und am Ende des Intervalls haben unterschiedliche Vorzeichen.
Bei der Intervallschachtelung wird das Intervall so verkleinert, dass die Nullstelle danach in dem verkleinerten Intervall liegt. Dieses Vorgehen wird wiederholt, bis das Intervall so klein ist, dass ein Wert aus dem Intervall als hinreichend genaue Näherung für die Nullstelle betrachtet werden kann.
Das Verkleinern das Intervalls erfolgt am bequemsten und schnellsten durch Halbieren. Diese spezielle Vorgehensweise wird Intervallhalbierungsmethode (Bisektionsmethode, Bild 2) genannt.
-
Intervallschachtelung
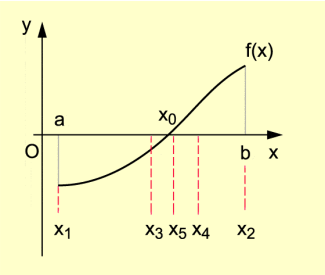
Das Intervall wird halbiert.
Die neuen Intervalle werden betrachtet.
Wegen des Vorzeichenwechsels im Intervall wird dieses Intervall für die Fortsetzung ausgewählt.
Für die Beendigung dieses Verfahrens muss eine Abbruchbedingung (eine Genauigkeitsforderung) angegeben werden.
-
Intervallhalbierungsmethode
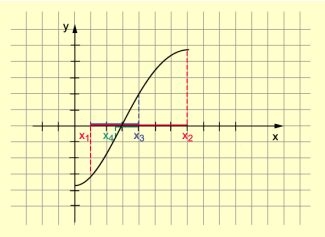
Das algorithmische Vorgehen zeigt das folgende Struktogramm:
![]()
Struktogramm der Intervallhalbierungsmethode

