Konstruieren mit Software
Der Computer ist in der Geometrie vor allem bei der Veranschaulichung komplexer Objekte und Sachverhalte hilfreich. Geeignete Software kann die Genauigkeit von Konstruktionen deutlich erhöhen.
Generell kann man zwischen statischer Geometriesoftware und dynamischer Geometriesoftware (DGS) unterscheiden.
Der Computer ist in der Geometrie vor allem bei der Veranschaulichung komplexer Objekte und Sachverhalte hilfreich.
Geeignete Software kann die Genauigkeit von Konstruktionen deutlich erhöhen. Sie beinhaltet spezifische Programmfunktionen wie beispielsweise:
- Rastereinstellungen mit definierbarer Einheit,
- Ausrichten an Rasterpunkten,
- Vergrößern der Ansicht der Zeichnung,
- Magnetisierbarkeit von Objekten (d. h., dass z. B. ein mit der Maus aktivierter Punkt unabhängig von geringen Abweichungen des Nutzers exakt getroffen und für die Zeichnung verwendet wird),
- Möglichkeit der genauen numerischen Eingabe von Winkelgrößen und Streckenlängen,
- integrierte Messfunktionen für Streckenlängen und Winkelgrößen
Darüber hinaus erleichtert Geometriesoftware das experimentelle Arbeiten und damit das Aufdecken von Gesetzmäßigkeiten.
Generell kann man zwischen statischer Geometriesoftware und dynamischer Geometriesoftware (DGS) unterscheiden.
Bei statischen Konstruktionsprogrammen kann man wie mit Zirkel und Lineal konstruieren. Das zeichnerische Können mit Zirkel und Lineal wird durch Können im Umgang mit Maus und Tastatur ersetzt.
Beispiele:
- KOBESCH
Programm, das in den 80ern Jahren entwickelt wurde,
Handhabung und Grafik nicht mehr zeitgemäß - KONZ
Win-Nachfolger von KOBESCH - Constri
komfortables und leistungsfähiges Win-Konstruktionsprogramm - Geocad
leistungsfähiges Konstruktionsprogramm (DOS und Windows 3.1)
Dynamische Geometriesoftware bietet darüber hinaus weitere Programmfunktionen. Hier ist es möglich, Makros selbst zu definieren und damit häufig wiederkehrende Zeichenaufgaben als Unterprogramme abzuspeichern. Vor allem aber lassen sich einmal gezeichnete Figuren im sogenannten Zugmodus dynamisch verändern.
Beispiele:
- Euklid – DynaGeo
völlig eigenständiges Programm; Zeichnungen lassen sich abspeichern und wieder laden, über Zwischenablage exportieren und ausdrucken; Folge von Konstruktionsschritten als Makros aufzeichnen, für ein zügiges Arbeiten sind ein schneller Rechner und eine leistungsfähige Grafikkarte erforderlich - Geonet
wurde in der Programmiersprache Java entwickelt; zeichnet sich durch folgende Merkmale aus: Zugmodus, Spurmodus, Messmodus, Rechenmodus
Zugmodus: ermöglicht das Bewegen von Punkten, Geraden oder anderen geometrischen Gebilden
Spurmodus: das Objekt hinterlässt auf der Zeichenfläche eine Spur, d. h., seine Ortskurve wird sichtbar
Damit lassen sich geometrische Zusammenhänge visualisieren. - Cinderella
Programm kann alles, was man mit Zirkel, Lineal und Dreieck auf einem Blatt Papier zeichnen kann.
Konstruktionen von einfachen Verbindungsgeraden, über Senkrechte, Winkelhalbierende und Parallelen bis zu Spiegelungen und auch Kegelschnitte sind mit diesem Programm ausführbar.
Einzelne Elemente einer Zeichnung kann man „anfassen“ und nach Belieben bewegen.
-
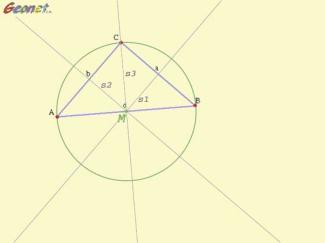
Umkreis eines Dreiecks