Geometrische Konstruktionen in der Physik
Beim Lösen bestimmter physikalischer Aufgaben (Zusammensetzung oder Zerlegung von Kräften, Zusammensetzung von Geschwindigkeiten, Zusammensetzung von Wegen) werden die Sachverhalte in einer maßstäblichen Zeichnung dargestellt und das Ergebnis durch geometrische Konstruktion ermittelt. Aus der geometrischen Konstruktion können dann weitere Folgerungen gezogen werden.
Beim Lösen bestimmter Aufgaben (Zusammensetzung oder Zerlegung von Kräften, Zusammensetzung von Geschwindigkeiten, Zusammensetzung von Wegen) werden die physikalischen Sachverhalte in einer maßstäblichen Zeichnung dargestellt und das Ergebnis durch geometrische Konstruktion ermittelt. Aus der geometrischen Konstruktion können dann weitere Folgerungen gezogen werden. Diese Art der Lösung wird insbesondere dann angewendet, wenn ausschließlich mit vektoriellen (gerichteten) Größen gearbeitet wird, wenn es also z. B. um Kräfte, Geschwindigkeiten, Wege oder Beschleunigungen geht.
Um solche Aufgaben zu lösen, kann man in folgenden Lösungsschritten vorgehen:
- Festlegen eines geeignetes Maßstabes für physikalische Größen
- Umrechnen der physikalischen Größen in Längen
- Grafische Darstellung des Sachverhalts unter Beachtung der Richtung der physikalischen Größen
- Durchführen der Konstruktion und Ermittlung des Betrages und der Richtung der physikalischen Größen
Beispiel:
Ein Segelboot bewegt sich immer in die Richtung, in welche die resultierende Kraft wirkt.
Wie groß ist die resultierende Kraft, wenn durch Westwind auf das Segel eine Kraft von insgesamt 250 N und gleichzeitig auf das Boot aufgrund einer nach Nordost verlaufenden Strömung eine Kraft von 100 N wirkt?
In welche Richtung bewegt sich das Boot aufgrund der resultierenden Kraft?
Analyse:
Auf das Segelboot wirken zwei Kräfte in unterschiedlichen Richtungen. Es kann angenommen werden, dass diese Kräfte an einem Angriffspunkt, dem Schwerpunkt des Bootes, angreifen. Mithilfe eines maßstäblichen Kräfteparallelogramms können Betrag und Richtung der resultierenden Kraft ermittelt werden.
-

linous - Fotolia.com
Lösung:
Für die maßstäbliche Zeichnung wird vereinbart:
1 cm 25 N
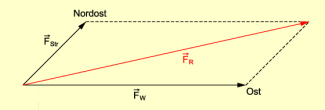
Damit hat der Kraftpfeil für die eine Kraft eine Länge von 10 cm und der für die andere Kraft eine Länge von 4 cm. Nun kann die Konstruktion unter Beachtung der Richtungen der Kräfte durchgeführt werden.
Der Kraftpfeil der resultierenden Kraft ist 13 cm lang. Die resultierende Kraft beträgt somit 325 N. Die Richtung ergibt sich aus der Skizze.
Ergebnis:
Die resultierende Kraft auf das Segelboot beträgt 325 N. Es bewegt sich in Richtung Nordnordost.
Die Lösung kann auch rechnerisch ermittelt werden.
-
Grafische Lösung
-
Rechnerische Lösung
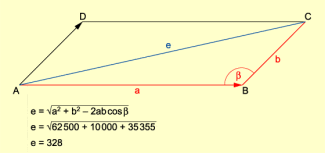
Eine weitere Lösungsmöglichkeit:
Um schnell zu einer Lösung solcher geometrischer Aufgaben zu kommen, kann man auch die nebenstehende Möglichkeit mithilfe des Programms „Geonet“ nutzen. Die Länge der Pfeile und ihre Richtung zueinander lassen sich verändern.

